为提高自由空间光(Free Space Optical, FSO)通信系统的传输速率，携带轨道角动量(Orbital Angular Momentum, OAM)的涡旋光束(Vortex Beams)越来越受到重视^[1]。涡旋光束是一类具有环形光强分布、螺旋波前结构的光束，在传输过程中，光束中心具有相位奇点，即在奇点处光强为零^[2]。由于不同阶次的OAM态相互正交，且本征态具有多维性，因此多路信息可在同一路径上传输，从而提高信道容量和频谱效率^[3]。涡旋光束已广泛应用于光通信、量子信息学、粒子捕获等诸多领域^[4-6]。

1992年，Allen等^[7]首次发现Laguerre-Gaussian(LG)模的光场是涡旋光，其光场表达式$\exp \left( {il\varphi } \right)$中，$l$为拓扑荷数或角向指数，对应光场中每个光子的OAM为$l\hbar $，$\hbar $为普朗克常数，$\varphi $为方位角。2012年，华中科技大学王健教授等^[8]提出并设计了一种基于OAM态复用的新型高速通信方式，其中四路不同OAM态编码16进制的正交幅度调制光信号，总传输速率可达1.37 Tbit/s。自此，OAM作为一种新型光复用的自由度引起广泛关注^[9]。然而，在实际基于OAM的FSO通信链路中，噪声，尤其是大气湍流对OAM态的干扰将是不可避免的，从而造成涡旋光束的螺旋波前发生畸变^[10]，降低了FSO通信链路的质量。另外，对于多路复用的涡旋光束，由于不同OAM态之间的分离依赖于螺旋相位前，湍流干扰也会导致接收端的OAM态间发生模间串扰，影响复用链路的通信性能^[11-12]。

在FSO通信系统中，造成接收端OAM光束的波前畸变的原因有很多，比如：光学器件、对准问题、湍流、非线性热效应以及流体特性等，其中大气湍流是最主要的影响因素^[13]。为了减轻湍流影响并提高通信性能，已经提出许多技术方案，这些方案通常可以分为抗湍流的空间模式^[14-15]、基于自适应光学(Adaptive optics, AO)的波前校正技术^[16-17]和空间分集技术^[18]。

文中介绍了涡旋光束的自适应光学波前校正技术，根据校正中是否使用波前传感器分为需要波前传感器和无需波前传感器两种类型，主要阐述各校正技术的基本原理，简述该技术的应用。另外，分析了水下湍流环境中涡旋光束的波前校正。

AO技术可以修复大气湍流等因素对光波波前造成的扭曲，在激光大气传输、光学测量、医学等领域得到了广泛应用^[19]。

基于AO的波前校正主要包括波前探测、波前控制和波前校正三个部分。波前传感器实时探测畸变波前信号，该信号经过波前控制子系统的处理得到波前控制的信号，并施加到波前校正子系统的变形镜来实现畸变波前的相位共轭补偿。图1显示了基于AO的波前校正技术，根据是否需要测量畸变相位的波前传感器分为两大类。由于经典的夏克-哈特曼(Shack-Hartmann, SH)波前校正技术^[20-22]需要用到波前传感器，属于需要波前传感器一类，而另一类不需要波前传感器，通过算法获取畸变波前，其中迭代算法有Gerchberg-Saxton(GS)相位恢复算法^[23-24]、随机并行梯度下降(Stochastic-Parallel-Gradient-Descent, SPGD)算法^[25-26]、遗传算法^[27]、模拟退火算法^[28]和利用深度学习进行波前校正的方法^[29-30]。

图  1  基于AO的校正技术

Figure 1.  Scheme of AO-based correction technology

下面将逐一描述各种基于AO的波前校正技术。

SH波前校正是通过SH波前传感器来实现的。SH波前传感器包括微透镜阵列和CCD(Charge coupled device)相机，入射光到达微透镜阵列时，CCD相机的像面上聚焦了微透镜焦点处的子波前。当波前为理想平面波时，CCD接收到一个理想的点阵；当入射光经过湍流发生波前畸变时，到达微透镜阵列的子波前会偏离焦点，CCD测得每个光斑的位置信息，得到子波前焦点的偏移量即可重构波前^[31]。2012年，笔者课题组研究了SH波前校正方法对FSO中大气湍流造成的波前畸变的校正^[32]，对于正交完备Zernike多项式函数，任意波前$\varphi \left( {x,y} \right)$可以由Zernike多项式${Z_0},{Z_1}, \cdots ,{Z_n}$的线性组合来描述：

式中：$\varphi \left( {x,y} \right)$为由大气湍流效应引起的畸变波前；${a_k}$为线性系数。得到方程组：

式中：$\varphi _x'\left( {x,y} \right)$和$\varphi _y'\left( {x,y} \right)$分别为$\varphi \left( {x,y} \right)$对$x$和$y$的偏导；$Z_{kx}'\left( {x,y} \right)$和$Z_{ky}'\left( {x,y} \right)$分别为${Z_k}\left( {x,y} \right)$对$x$和$y$的偏导。公式(2)也可写成如下矩阵的形式：

式中：${G_x}\left( m \right) = \varphi _x'\left( m \right)$，${G_y}\left( m \right) = \varphi _y'\left( m \right)$；${D_{kx}}\left( m \right) = Z_{kx}'\left( m \right)$和${D_{ky}}\left( m \right) = Z_{ky}'\left( m \right)$。则公式(3)可简化为：

解出Zernike多项式系数：

因此，可以通过公式(1)和(5)得到畸变波前的估计相位。

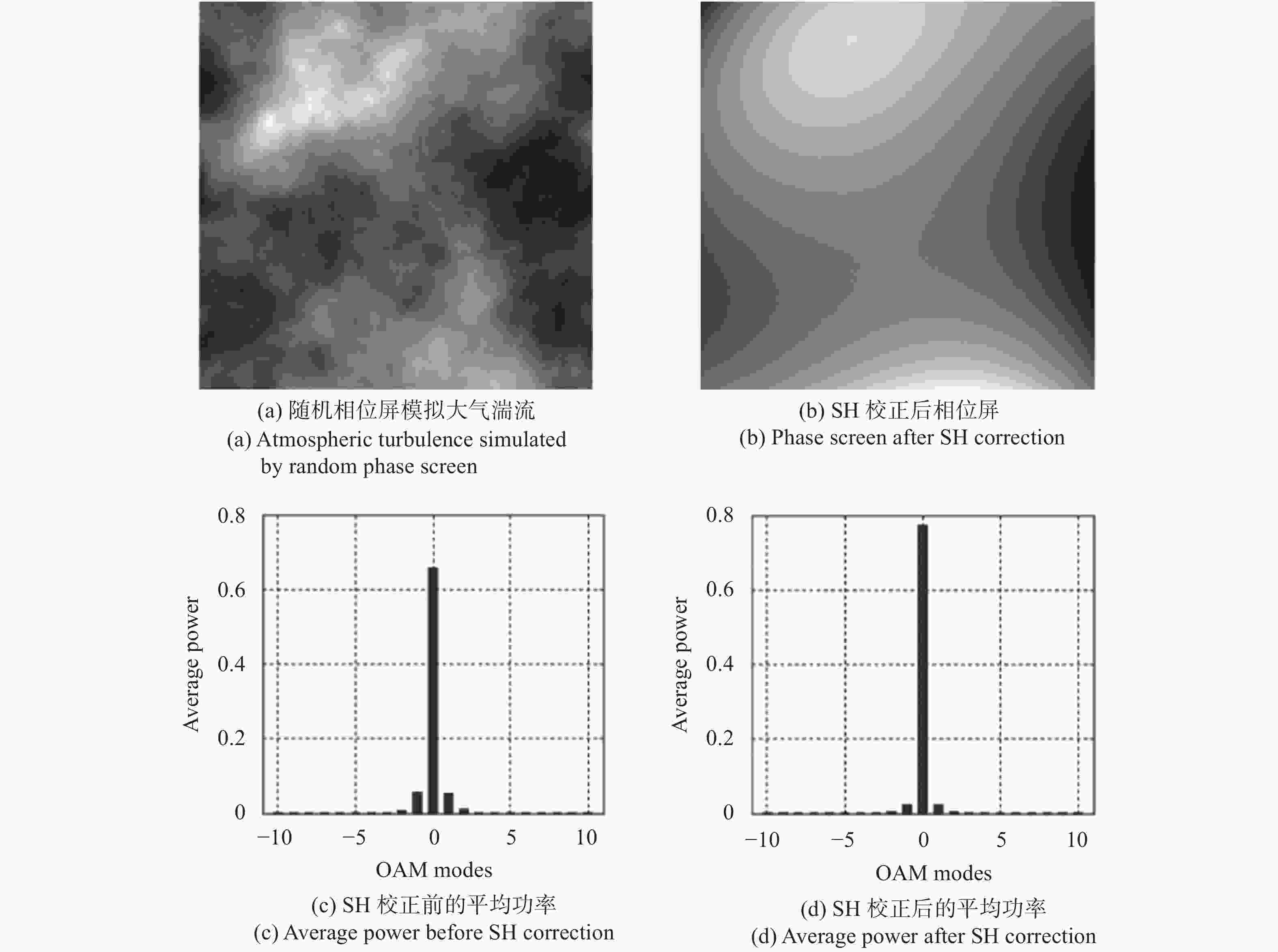
图2显示了SH算法的校正效果，其中图2(a)为仿真大气湍流产生的随机相位屏，图2(b)为SH算法重构后的相位屏，图2(c)和图2 (d)分别显示了LG模式(OAM $l = 0$)经过AO校正前后的模式分布情况。结果表明，SH算法可以有效获取仿真大气湍流的相位分布，校正后OAM $l = 0$光束的平均功率由65%提升到77%，湍流引起的波前畸变得到了有效的校正。

图  2  SH算法的校正效果^[32]

Figure 2.  Correction effect of SH algorithm^[32]

考虑到OAM光束存在相位奇点，导致有些位置的波前不易探测。2014年，Ren^[33]等人利用探测光束来检测波前畸变，即将偏振正交的高斯光束和OAM光束通过偏振光分束器合束，然后同轴传输经过大气湍流，接收端用另一个偏振光分束器将合束分离，波前传感器探测到畸变的高斯光束，同时得到了OAM光束的波前畸变信息。分离出的高斯光束进入AO闭环校正系统得到校正相位，加载到两个波前校正器上，从而完成对高斯光束和OAM光束的校正。

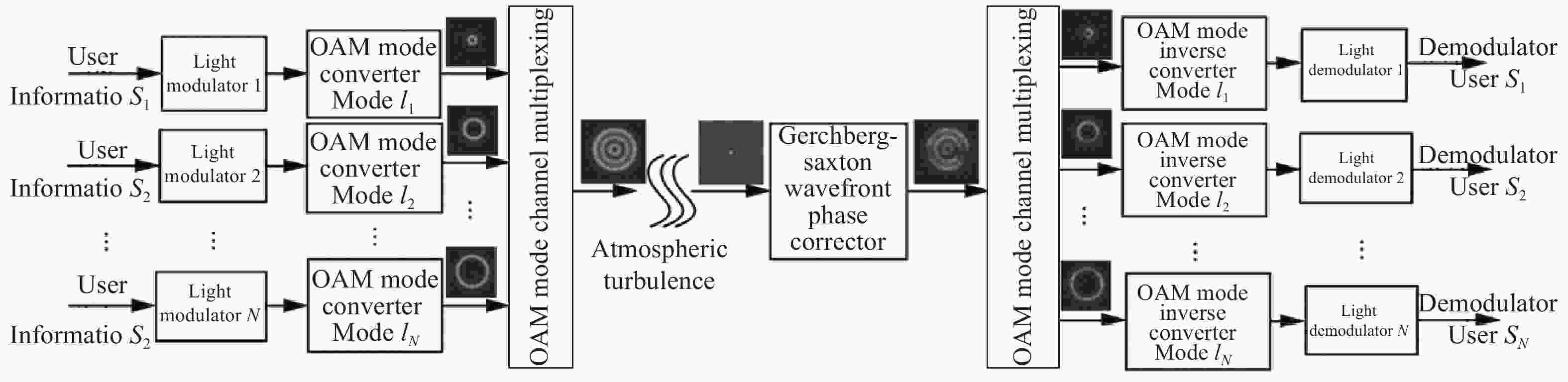
GS算法是一种相位反演的迭代算法，图3为GS相位恢复算法流程图。由湍流和原始高斯探测光束的平坦相位${\varphi _0}$提取原始畸变高斯光束的振幅${a_0}$，初始光场为${a_0}\exp \left( {i{\varphi _0}} \right)$；然后进行快速傅里叶变换(Fast Fourier transform, FFT)，得到中间过程的频谱函数${A_0}\exp \left( {i{\varphi _1}} \right)$；将振幅${A_0}$替换为原始高斯光束的振幅${B_0}$，保留相位${\varphi _1}$，得到新的频谱函数$U = {B_0}\exp \left( {i{\varphi _1}} \right)$；对$U$进行快速傅里叶逆变换(Inverse fast Fourier transform IFFT)，得到振幅和相位函数${b_0}\exp \left( {i{\varphi _2}} \right)$；继续用原始畸变高斯光束的振幅${a_0}$代替${b_0}$，同时保留相位${\varphi _2}$，得到$u = {a_0}\exp \left( {i{\varphi _2}} \right)$；将更新的相位函数替换为误差函数，根据误差精度可以判断循环迭代是否继续，直到满足误差精度时得到所需相位${\varphi _2}$。

图  3  GS相位恢复算法流程图

Figure 3.  Flow chart of GS phase recovery algorithm

笔者课题组提出了一种基于GS波前相位校正算法抑制大气湍流对OAM态复用FSO通信系统干扰的方案^[17]，校正模型如图4所示。该算法利用扭曲的OAM态复用光幅度，通过迭代运算得出大气湍流干扰引起的畸变相位，然后将OAM态复用光相位与其相减，从而达到降低大气湍流干扰导致OAM态复用光相位扭曲的程度。此外，还通过仿真和实验比较了SH算法和GS算法在相同大气湍流下对畸变OAM畸变波前的校正效果^[21]，从图5可以看出，大气湍流导致OAM态模间串扰，SH和GS两种算法均能校正波前畸变，提高OAM态光束质量，且GS算法具有较好校正波前畸变的性能。

图  4  GS算法校正OAM态复用系统的大气湍流干扰^[17]

Figure 4.  GS algorithm corrects atmospheric turbulence interference in OAM state multiplexing system^[17]

2016年，北京理工大学的高春清团队提出利用高斯探测光束结合GS相位恢复算法对OAM光束波前进行预校正的技术^[24]。原理是具有独立偏振方向的基模高斯光束作为探测光束与OAM光束同轴传输，受到大气湍流干扰后，从OAM光束的畸变强度及GS算法获得校正相位图，然后使用校正相位模式来预校正畸变OAM光束。

图  5  大气湍流干扰校正前后的探测概率^[21]

Figure 5.  Decomposition of the beam after passing through atmospheric turbulence with and without a correction^[21]

1998年，美国海军实验室的M.A.Vorontson和新墨西哥州的V.P.Sivokon设计了SPGD算法用于高分辨率的AO波前校正^[34]。该算法利用性能函数寻找最佳相位面，根据相位共轭原理对光束进行修复。性能函数包括了斯特列尔比(Strehl Ratio, SR)、光学传递函数(Optical Transfer Function, OTF)、像清晰度函数等。SPGD算法也是无波前传感器的AO优化算法，不同于传统的基于梯度的无模型优化算法，SPGD算法使用的梯度估计方法兼具串行扰动法和多通道小抖动法的优点，称之为随机并行扰动法。

SPGD算法也是一种需要迭代的波前校正方法，图6为SPGD算法的第(k+1)次迭代框图。具体实现步骤可描述如下^[35-36]：

图  6  SPGD算法第(k+1)次迭代^[35]

Figure 6.  The (k+1)th iteration of the SPGD algorithm^[35]

(1) 电压参量初始化：变形镜驱动器的电压控制信号清零，${U_0} = \left[ {{u_1},{u_2},\cdots,{u_N}} \right],{u_i} = 0,i = 1,2,\cdots,N$。

(2) 算法迭代计算：已知SPGD算法当前校正模式，即第k次迭代所得的电压信号矩阵为${U_k} = $$ [{u_{1,k}},{u_{2,k}},\cdots,{u_{N,k}}]$。产生扰动量分别为$ + \Delta {U_k}$和$ - \Delta {U_k}$的正向和反向扰动电压，通过控制模块将电压${U_k} - $$ \Delta {U_k}$和${U_k} - \Delta {U_k}$施加给变形镜，然后采集光斑信息，获得光强分布，分别计算得到系统目标函数值${C_{1,k}}$和${C_{2,k}}$。${C_k} = \displaystyle\int_0^1 {\displaystyle\int_{ - \pi }^\pi {I\left( {r,\theta } \right)} } {I_{id}}\left( {r,\theta } \right){\text{d}}\theta {\text{d}}r$,$I\left( {r,\theta } \right)$为实际远场光强分布，${I_{id}}\left( {r,\theta } \right)$为理想情况下的光强分布。下一次变形镜上施加的电压参量取值为${U_{k + 1}} = {U_k} + \mu \Delta {U_k}( {{C_{1,k}} }- $$ {{C_{2,k}}} )$，其中，$\Delta {U_k} = \left[ {\Delta {u_{1,k}},\Delta {u_{2,k}},...,\Delta {u_{N,k}}} \right]$，$\mu $为增益系数，为电压的随机扰动量，$\Delta {u_{i,k}}$满足伯努利分布且相互独立。

(3) 电压参量更新：将当前变形镜所施加的电压值更新为${U_{k + 1}}$。

2013年，Xie等人^[25]提出了一种基于Zernike多项式的SPGD算法用于畸变OAM光束的相位校正。其原理是将畸变OAM光束的强度分布通过SPGD算法循环迭代得到校正图案的Zernike多项式系数，然后控制波前校正器，从而实现OAM光束的畸变校正。实验结果表明，该方法可以同时校正通过同一湍流的多路OAM光束，并且将模间串扰减少了5 dB以上。

除了GS算法和SPGD算法之外，其他无需波前传感器的AO校正方法还包括遗传算法、模拟退火算法。

2007年，中国科学院光电技术研究所姜文汉院士团队在遗传算法的基础上，提出了一种实数编码的高斯变异的遗传算法，并利用该算法仿真控制61单元变形镜校正由前35阶Zernike多项式表述的波前畸变^[27]。该算法在不测量波前畸变的条件下，经过1000次迭代运行后，利用高斯变异遗传算法可以找到变形镜校正波前畸变的最佳面形，该算法收敛性很好，波前畸变得到校正后，光束的峰值光强和能量集中度都有很大提高。

2011年，国防科技大学余湛等人^[28]在模拟退火算法的基础上，结合Zernike模式法，对算法的初始相位、扰动方式和评价函数进行改进，通过改进加快了算法的收敛速度，得到了匀滑的相位屏，使得模拟退火算法可以适用于OAM光束的波前畸变。

另一方面，由于算法本身的局限性，遗传算法和模拟退火算法在波前畸变校正中的应用不如前文所介绍的校正方法广泛，但两种算法作为常用的全局搜索算法为校正OAM光束波前畸变拓展了研究思路。

传统的AO方法不具备学习和记忆能力，GS算法和SPGD算法有可能会收敛于局部最小值，不能达到最佳校正效果。近年来，随着机器学习的快速发展，尤其是基于数据驱动的深度学习技术让人工智能得到了全面关注。传统的机器学习以其原始形式处理自然数据的能力受到限制，深度学习算法与传统机器学习算法之间的最大区别在于模型的容量，而较深的模型意味着更好的拟合能力^[37]。深度学习技术在图像识别和分类方面显示出非凡的能力，在光学领域引起了广泛的关注^[38]。

波前畸变可以利用一系列Zernike多项式的线性组合来表示。入射的高斯光束经过大气湍流后发生畸变，导致了Zernike多项式对应的系数发生改变。卷积神经网络(Convolutional neural network, CNN)模型可以直接将CCD记录的强度图像映射到Zernike系数，然后使用传输模块将Zernike系数转换为DM的控制信号。如图7所示，经过大气湍流后的畸变光束通过透镜聚焦，并由CCD记录，并与对应的Zernike系数构成数据集，通过CNN进行训练，然后输入一张畸变的强度图，经CNN模型后得到预测的Zernike系数，最后反馈到控制器，控制器可以调整DM的控制信号以校正波前畸变。

图  7  利用CNN校正波前畸变的无传感器AO系统

Figure 7.  Sensor-less AO system using CNN to correct wavefront distortion

2019年，Tian等人^[39]将深度学习应用到波前畸变校正，直接利用了OAM光束强度分布检测波前畸变，从而避免迭代的耗时和陷于局部最优的问题。该模型结构共有七个卷积层用来提取输入图像的特征；卷积核的大小设置为3×3；一些卷积层后面是步长为2的池化层，用来降维、去除冗余信息、对特征进行压缩、简化网络复杂度；模型结构最后是三个全连接层，将学到的“分布式特征表示”映射到样本标记空间，最终输出强度分布图像对应的前2~400阶Zernike系数，然后将这些系数转换为控制信号，并模拟DM来校正畸变。

基于CNN的校正技术从畸变的强度图像中提取特征，并通过CNN获得相应的Zernike系数。同年，Ma^[40]等人设计了基于CNN的模型用来校正波前畸变。模型训练和输出的过程如下：两个在焦距和离焦距上的畸变强度图像以及对应湍流相位屏的Zernike系数组成的数据集被输入到模型的训练算法中；训练后，该模型将获得两个强度图像以生成预测的Zernike系数。结果表明基于CNN的AO校正方法可预测相位的Zernike系数，极大地改善了波前残留方差，且不需要波前检测和相应的重建计算，也不需要在实际系统中进行迭代优化。

考虑到大气湍流可以用相位屏来模拟，所以建立强度图像和相位屏的映射关系亦能校正大气湍流对涡旋光束造成的畸变。2019年，Liu^[41]等人设计了一种CNN模型，该模型学习输入强度分布与湍流相位的映射关系，经过大量样本训练后CNN模型具有良好的泛化能力，快速准确地预测等效的湍流相位屏，包括未训练的湍流相位屏。CNN模型结构的输入是原始高斯光束和受大气湍流影响的强度分布，经过12层卷积和3层反卷积（也被称作“转置卷积”，对特征图进行上采样，保证输出图片与原始图片大小相同）后输出大气湍流的相位屏。输入和输出的图像大小为64×64，输出的相位屏与真实的作对比，误差最小时输出最终结果。提取畸变相位信息后，通过向畸变光束加载反相位来校正波前畸变。

2020年，北京理工大学的高春清团队建立了一个基于深度学习的自适应光学系统，从相位分布和模式纯度来补偿矢量涡旋光束的湍流像差^[42]。该团队设计了一种基于CNN的湍流像差校正模型，该模型通过实验实例学习了畸变矢量涡旋光束的强度分布与前20阶Zernike产生的湍流相位的映射关系，预测得到补偿的相位，从而实现矢量涡旋光束的校正。该方案将深度学习和自适应光学领域相结合，对结构光束的通信和成像有很大帮助。

基于CNN模型的AO校正系统具有结构简单、易于实现、成本低、系统带宽高等优点。但在训练过程中，卷积核的大小、卷积层的深度、评价函数、模型优化算法等诸多因素都会影响系统的稳定性、准确性和泛化能力。因此，在以后的研究中有必要考虑这些因素来优化和改进模型。

随着对水下数据传输的需求不断增长，例如潜艇、自动驾驶水下航行器和无人驾驶水下航行器，水下无线光通信(Underwater wireless optical communication, UWOC)作为水下环境的潜在技术引起了人们的极大兴趣^[43]。与射频和声波通信相比，UWOC具有传输带宽高、传输速率快、链路延迟低、安全性高和成本低等优点^[44]。为了增加系统容量，OAM也被引入到UWOC系统中，携带OAM的涡旋光被广泛应用于自由空间和水下复用通信系统^[45]。但是，涡旋光束在水下传输时同样会受到水下湍流的影响。水下湍流指的是由于流体的运动、温差等因素引起的介质折射率在时间和空间位置上随机变化的现象，携带信息的涡旋光束在水下环境中传输时，湍流导致的强度衰减、相位畸变会影响通信质量。因此，校正涡旋光束在水下传输时受到湍流的影响尤为重要^[46]。

为了研究水下湍流中涡旋光束的校正，笔者课题组通过数值仿真的方式构建了基于功率谱反演法的水下湍流相位屏模型，通过次谐波补偿的方式弥补了该方法低频成分不足的缺陷，并利用相位结构函数验证了其正确性，最后通过改进的水下湍流模型研究了LG光束在水下湍流中的传输特性^[47]。

另外，笔者课题组利用改进的水下湍流模型通过实验比较了经典的三种AO方法，包括SH、SPGD、GS算法^[48]。实验过程是将三个不同拓扑荷值(−3、0、+5)的涡旋光束通过水下湍流相位屏，在接收端探测得到传输概率。从传输概率可以得出，水下湍流对涡旋光束在UWOC系统中的传输产生了较大的影响，降低了通信性能。在相同的水下湍流干扰下，GS算法的校正效果最好，SPGD算法较好于SH校正方法。

在涡旋光束的自适应光学波前校正技术中，SH波前校正方法需要用到波前传感器；而无需波前传感器的SPGD算法和GS相位恢复算法则需要进行迭代计算，校正效果较好，收敛速度较快，但容易陷于局部极值；遗传算法和模拟退火算法编程实现比较复杂且收敛速度较慢；结合深度学习的波前校正方法不用迭代，且节约大量时间，但数据集的制备、模型的设计、优化算法的选择都会影响校正效果。总之，这些方法都可以实现涡旋光束的波前校正，为涡旋光束在通信系统中的应用提供保障。

随着计算机数据处理能力的快速提高，可以预见结合深度学习的波前校正方法会成为新的研究热点。在保证校正速度、精确度的前提下能够节约成本，适应各种复杂通信环境（强湍流或者水下通信）的校正技术将是未来研究的重点，所以未来充满了机遇和挑战。