-
1970年,Alfano等人首次报道了在块状玻璃中可以产生超连续谱[1-2]。超连续谱产生是一种复杂的非线性现象,一般是高峰值功率超短脉冲通过非线性介质(典型的是光纤)产生。超连续谱在频谱分析[3]、高精度光频率测量[4-5]、光纤通信[6-7]等领域有着巨大的应用。在非线性介质中产生超连续谱主要经历三个过程:首先,由于自相位调制,输入脉冲经历了频谱压缩过程。其次,脉冲的峰值上升到一定的强度,其频谱在脉冲中心周围对称地扩大;此外,由于反常色散,长波长区域的孤子逐渐演变成高阶孤子,在短波长处产生色散波(蓝移色散波)。相应地,根据相位匹配条件,高阶孤子分裂产生了能量,成为共振非孤子辐射(切伦科夫辐射)[8-10]。最后,在高阶色散和非线性效应的共同影响下,高阶孤子分裂并成为多个基阶孤子[11]。超连续谱产生也与所选取的材料有关系,一般选取的材料有硫系折射率光纤[12]和光子晶体光纤。光子晶体光纤是一种硅质光纤,沿其长度排列着有序的微观气孔。光纤的导向特性是由空穴和固体二氧化硅区域的大小和模式决定的,而不是像传统光纤那样由大块光学玻璃的特性决定的。光子晶体光纤的色散特性是通过改变光纤内部的结构,可以得到具有多个零色散点的光纤[13-14]。
随着非线性光学不断发展,许多新型光脉冲逐渐被人们发现。不同的光脉冲在光子晶体中产生的超连续的形状和宽度各不相同,从而丰富了超连续谱理论。众所周知,Airy脉冲具有一些奇异特性,如无衍射[15]、横向加速[16]和自愈特性[17],在高阶非线性介质中具有更大的频谱宽度[18],主峰和旁瓣均可以出现小尺度自聚焦[19]。
并在许多领域具有重要的应用前景,如光学显微操作[20]、等离子体物理[21]、光学开关[22]、光学俘获[23]和光学路由[24]等。最近,通过用cosh函数调制Airy脉冲,产生了一种新的类Airy脉冲[25],即cosh-Airy脉冲。它在控制脉冲的轮廓方面比基本Airy脉冲具有更大的自由度[26]。cosh-Airy脉冲可以看作是两个具有不同截断系数的Airy脉冲的叠加[27],并且具有与Airy脉冲相似的传输特性。目前,研究者主要研究了cosh-Airy脉冲在光轴正交[28]的单轴晶体中的传输特性,并发现了cosh-Airy脉冲的自愈能力高于Airy脉冲[29]。对于具有更高自由度的cosh-Airy脉冲,其特征参数如何影响超连续谱,目前研究甚少,并且脉冲在双零色散介质传输时,可以产生比单零色散介质平坦性更高的超连续谱,因此文中主要研究cosh-Airy脉冲在双零色散介质中的传输特性和超连续谱产生,并找到操控超连续谱的方法。
-
cosh-Airy脉冲在双零色散介质中传播,可以用非线性薛定谔方程[26]来描述:
$$ \begin{split} \frac{{\partial U\left( {Z,T} \right)}}{{\partial Z}} =& \sum\limits_{k \geqslant 2} {\frac{{{i^{k + 1}}}}{{k!}}} {\beta _k}\frac{{{\partial ^k}U}}{{\partial {t^k}}}{\text{ + }}i\gamma \left( {1 + \frac{i}{{{\omega _0}}}\frac{\partial }{{{\partial _T}}}} \right) \times\\ &\left[ {U\left( {Z,T} \right)\int_{{{ - }}\infty }^{{\text{ + }}\infty } {R\left( {T'} \right){{\left| {U\left( {Z,T - T'} \right)} \right|}^{\text{2}}}} {\rm{d}}T'} \right] \end{split}$$ (1) 式中:U=U(Z, T)表示的是复电场包络的振幅;T表示在参考系中脉冲群速度的时间变量;Z表示传输距离;βk和γ表示第k阶色散和非线性系数,并且非线性系数为γ=n2ω0/(cAeff),n2表示熔融石英玻璃的非线性折射率,数值大小大约为2.0×10−20 m2/W,并且ω0和Aeff分别表示输入脉冲频率和非线性介质的有效模式面积。色散效应由公式(1)右边的第一项描述,而自相位调制、受激拉曼散射和自陡化等非线性效应对应于第二项。色散系数βk可以展开为12级的多项式。公式(1)右边的第二项中R(T)为响应函数,包括了电学和振动的拉曼响应,假设电学的影响几乎是瞬时的,R(T)函数的表达式为:
$$ R\left( T \right) = \left( {1 - {f_R}} \right)\delta \left( T \right){\text{ + }}{f_R}{h_R}\left( T \right) $$ (2) 式中:fR表示延时拉曼响应对非线性极贡献,数值一般约为0.18;δ(T)表示单位脉冲响应。
${h_R}\left( T \right)$ 函数的表达式为[30-31]:$$ {h_R}\left( T \right) = \frac{{\tau _1^2 + \tau _2^2}}{{{\tau _1}\tau _2^2}}\exp \left( { - \frac{T}{{{\tau _2}}}} \right)\sin \left( { - \frac{T}{{{\tau _1}}}} \right) $$ (3) 式中:τ1=0.122 s和τ2=0.032 s表示拉曼响应中两个可调参数。公式(1)中存在时间导数项可以视作为一个扰动。通过使用一个新的函数B(Z, T)[32]可表示为:
$$ B\left( {Z,T} \right) = A\left( {Z,T} \right)\exp \left[ {i\gamma \cdot R\left( T \right){{\left| {{A_0}} \right|}^2} \cdot \left( {Z - {Z_0}} \right)} \right] $$ (4) 结合分步傅里叶法和四阶Runge-Kutta积分法进行数值计算,函数表示为:
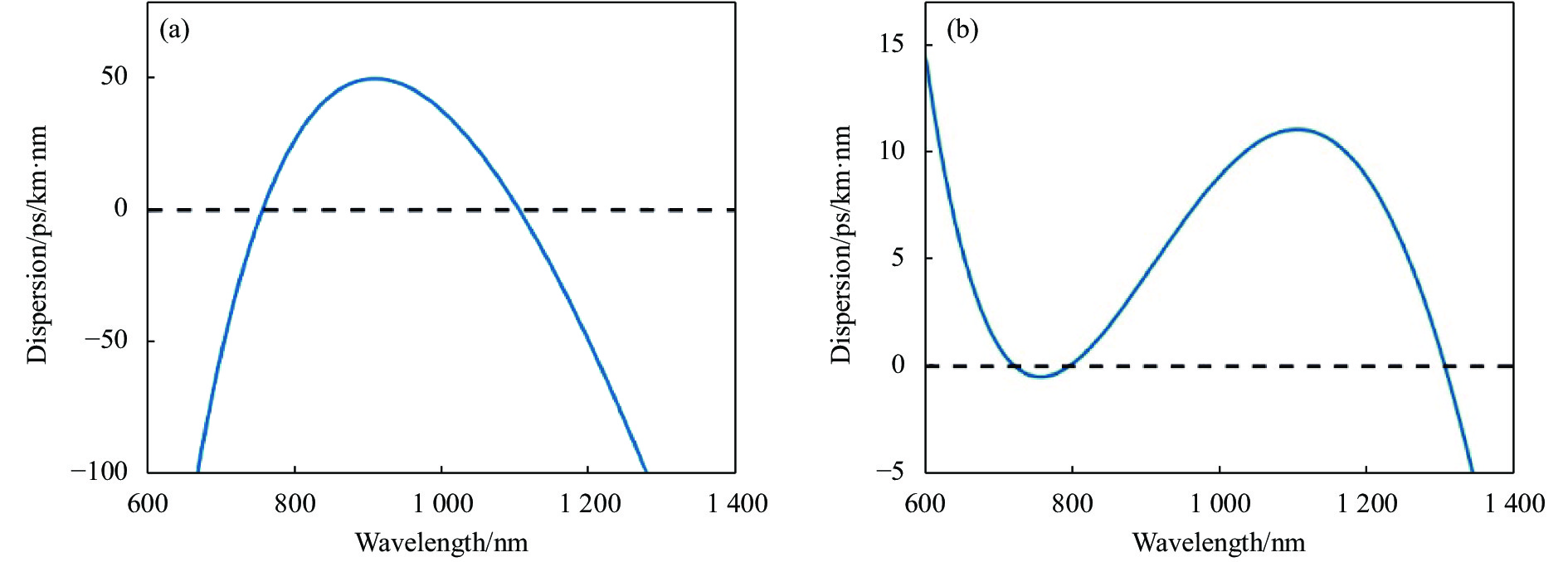
$$ \frac{{\partial B\left( {Z,T} \right)}}{{\partial Z}} = i\gamma B \cdot R\left( T \right) \cdot \left( {{{\left| {{B_0}} \right|}^2} + {{\left| B \right|}^2}} \right) - \frac{\gamma }{{{\omega _0}}} \cdot \left[ {B \cdot R\left( T \right) \cdot {{\left| B \right|}^2}} \right] $$ (5) 利用四阶Runge-Kutta分法可以求解公式(5),通过公式(4)可以得到A(z,t),结合分步傅里叶方法可以精确求解公式(1)。根据参考文献[32-33]中的方法设计一个双零色散介质,产生超连续中心波长大约在1 064 nm,较低波长的零色散点为756 nm,较高波长的零色散点为1 106 nm,非线性系数为γ=0.11 W·m−1和所使用的12阶色散系数为:β2=−8.0352×10−3 ps2/km, β3=6.2527×10−5 ps3/km, β4=−605314×10−9 ps4/km, β5=−3.3086×10−10 ps5/km, β6=1.2379×10−13 ps6/km, β7=−4.3681×10−15 ps7/km, β8=1.7687×10−17 ps8/km, β9=−8.9723×10−19 ps9/km, β10=4.9736×10−22 ps10/km, β11=−2.5042×10−25 ps11/km, β12=5.7033×10−26 ps12/km。图1(a)~(b)所示为双零色散介质的色散分布图曲线图和相对群延迟随频率的变化曲线图。从图中可以看出,色散分布曲线与零色散有两个交点,刚好将色散面分为左、右两个反常色散区域,中间为正常色散区。在双零色散介质中所获得的超连续谱形状也比单零色散介质生产的更平坦、更有使用价值。由于数值模拟所考虑的双零色散介质长度较短,所以忽略损耗。
图 1 (a) 双零色散介质的色散分布曲线,(b) 和相对群延迟曲线
Figure 1. (a) Dispersion distribution curve, (b) Relative group delay curve of the double-zero dispersive media
采用cosh-Airy脉冲为初始输入脉冲,其具有如下形式:
$$ U\left( {Z = 0,T} \right) = \sqrt {{P_0}} Ai\left( T \right)\exp \left( {aT} \right)\cosh \left( {{\chi _0}T} \right) $$ (6) 式中:
${P_0}$ 为峰值功率;$Ai$ 表为Airy函数;a为截断系数;C为cosh-Airy脉冲的初始啁啾;χ0为分布因子。cosh-Airy脉冲可以看做是两个不同衰减因子的Airy脉冲叠加的结果,可表示为:cosh-Airy脉冲可以看做是两个不同衰减因子的Airy脉冲叠加的结果,可表示为:
$$\begin{split} &U\left( {Z = 0,T} \right) =\\ &\frac{1}{2}\left[ {\sqrt {{P_0}} Ai\left( T \right)\exp \left( {{a_ + }T} \right) + \sqrt {{P_0}} Ai\left( T \right)\exp \left( {{a_ - }T} \right)} \right] \end{split} $$ (7) 其中
$$ \begin{split} \\ {a_ + } = a + {\chi _0} \end{split} $$ (8) $$ \begin{split} \\ {a_ - } = a - {\chi _0} \end{split} $$ (9) 从公式(9)中可以看出,要获得有限能量的cosh-Airy脉冲,需要取
$ {a_ - } = a - {\chi _0} $ >0。当分布因子χ0为0时,公式(7)描述的为Airy脉冲。具有初始啁啾的cosh-Airy脉冲,其表达式为:$$ \begin{split} &U\left( {Z = 0,T} \right) = \\ &\sqrt {{P_0}} Ai\left( T \right)\exp \left( {aT} \right)\exp \left( { - iC{T^2}} \right)\cosh \left( {{\chi _0}T} \right) \end{split}$$ (10) 图2所示为输入峰值功率为5 kW、截断系数为0.1的无啁啾cosh-Airy脉冲的波形图和频谱图。从图2(a)中可以看出,随着χ0的增加其旁瓣的能力逐渐增加,主峰的强度变化不大。
-
文中详细讨论了cosh-Airy脉冲在双零色散介质中的传输特性,cosh-Airy脉冲的中心波长为1064 nm,脉冲宽度为0.05 ps,介质长度为0.4 m。当P0=5 kW,a=0.3,C=0,χ0=0.15时,图3所示为cosh-Airy脉冲在双零色散介质中经过六个不同的传输距离时的波形和频谱演化情况。从时域波形图中可以看出,cosh-Airy脉冲的主峰和少数旁瓣经历了孤子分裂和线性偏转(见图3(a1~f1))。从频域光谱图可以看出cosh-Airy脉冲在双零色散介质中经历了初始展宽、剧烈展宽和饱和展宽一系列的过程:cosh-Airy脉冲在传输的初始阶段,由于自相位调制的作用,cosh-Airy脉冲的频谱将产生子峰,随后其频谱在脉冲中心周围对称地扩大(见图3(b2)),这是因为光子晶体光纤具有高阶色散。cosh-Airy脉冲在高阶色散的作用下将会诱导线性频率啁啾,线性频率啁啾将展宽脉冲频谱;在传输距离大约为0.06 m时,脉冲完成了压缩过程,主峰能量达到了最大值而变成高阶孤子,这些具有高能量的孤子随后分裂,导致频谱宽度急剧增加,并在短波长区域产生色散波(见图3(c2));脉冲的中心波长区域处于正常色散区域,高阶孤子将会进一步分裂,而短波长处于反常色散区,将会产生一定的蓝移色散波(见图3(d2));最后当产生的高阶孤子最多和色散波展宽到最大后,cosh-Airy脉冲达到超连续谱的饱和宽度而稳定的传输。
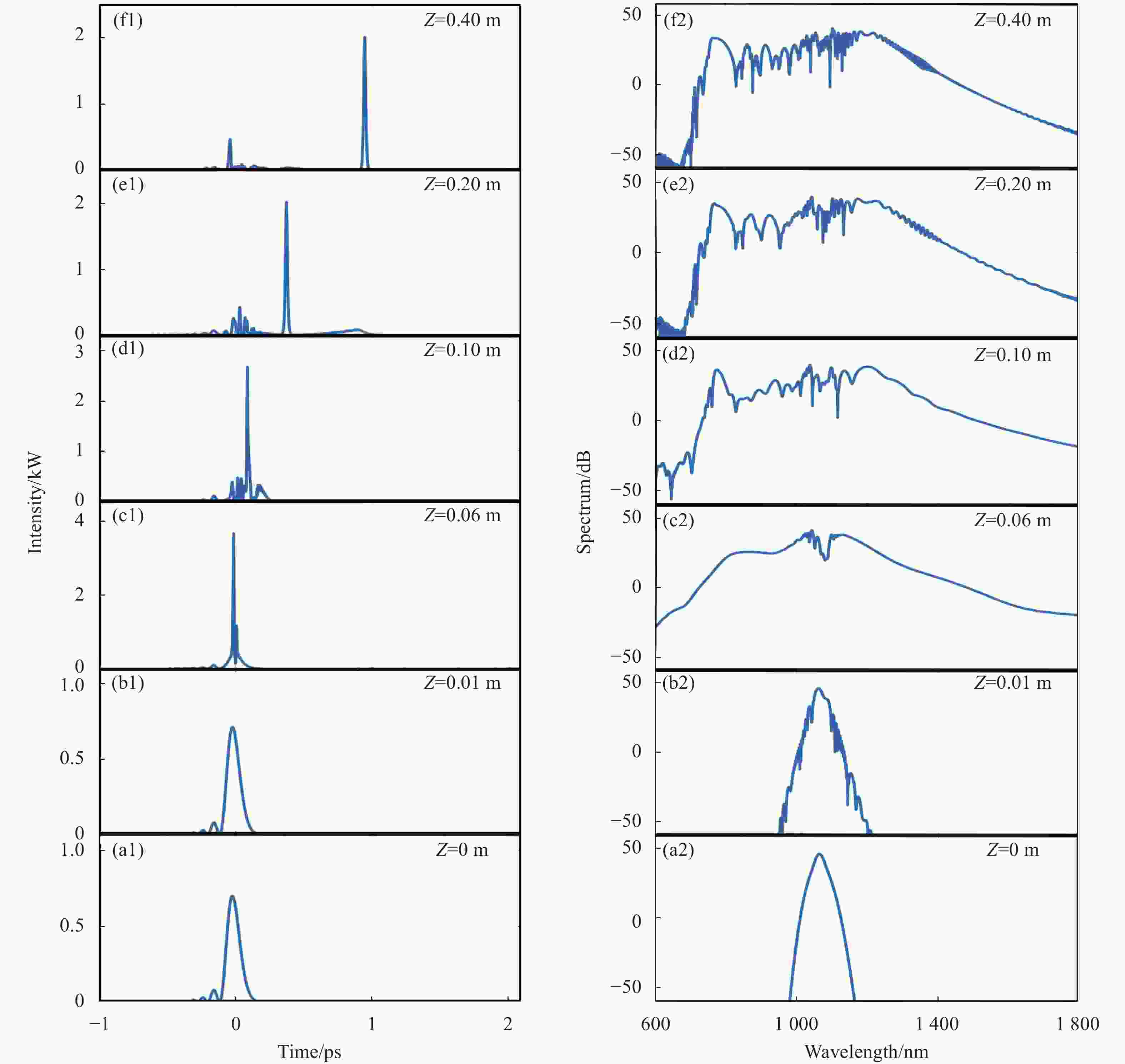
图 3 双零色散介质中,不同传输距离的cosh-Airy脉冲的波形图(左列)和频谱图(右列)
Figure 3. Waveform (left column) and spectrum (right column) of cosh-Airy pulses at different distances in a double-zero dispersion medium
截断系数a是控制cosh-Airy脉冲的波形的一个自由度,为了探究截断系数对cosh-Airy脉冲产生超连续谱的影响,开展了数值模拟研究。当P0=5 kW,C=0,χ0=0.15时,图4所示为不同截断系数的cosh-Airy脉冲在双零色散介质中的时域和频域演化情况。从时域演化图来看(图4(a1)~(c1)):Airy脉冲为多峰结构,截断系数a 能够控制旁瓣的能量大小;a为0.2时,Airy脉冲有许多振荡拖尾的旁瓣 (图4(a1));当a增大时,脉冲振荡拖尾部分的旁瓣迅速减少, 而脉冲总能量不变,即拖尾旁瓣能量转移到了主峰(图4(b1)~(c1))。cosh-Airy脉冲在双零色散介质中传输,受到高阶色散和Kerr非线性效应的共同作用。对于截断系数更大的cosh-Airy脉冲,由于其主峰的能量占比更大,其受到的非线性效应更大,高阶色散对主峰产生的高阶孤子的偏转效应就更小。从频域演化图来看,当截断系数a=0.2时,cosh-Airy脉冲所产生的超连续谱的宽度稳定在752 nm (图4(a2)),随着截断系数从0.2增加到0.5,所产生的超连续谱的宽度逐渐减小(图4(a2)~(c2))。特别值得注意的是:当截断系数a=0.5时,随着传输距离的增加,cosh-Airy脉冲产生超连续谱的宽度出现了一定程度的减小。由以上分析可知,发现可以通过选取不同的截断系数来控制cosh-Airy脉冲产生超连续谱的宽度。随截断系数的增加,从cosh-Airy脉冲在传输距离为0.4 m处的波形图(图4(d1))和频谱图(图4(d2))同样可以看出其时域脱落孤子的线性偏转减小和频域超连续谱的宽度减小。
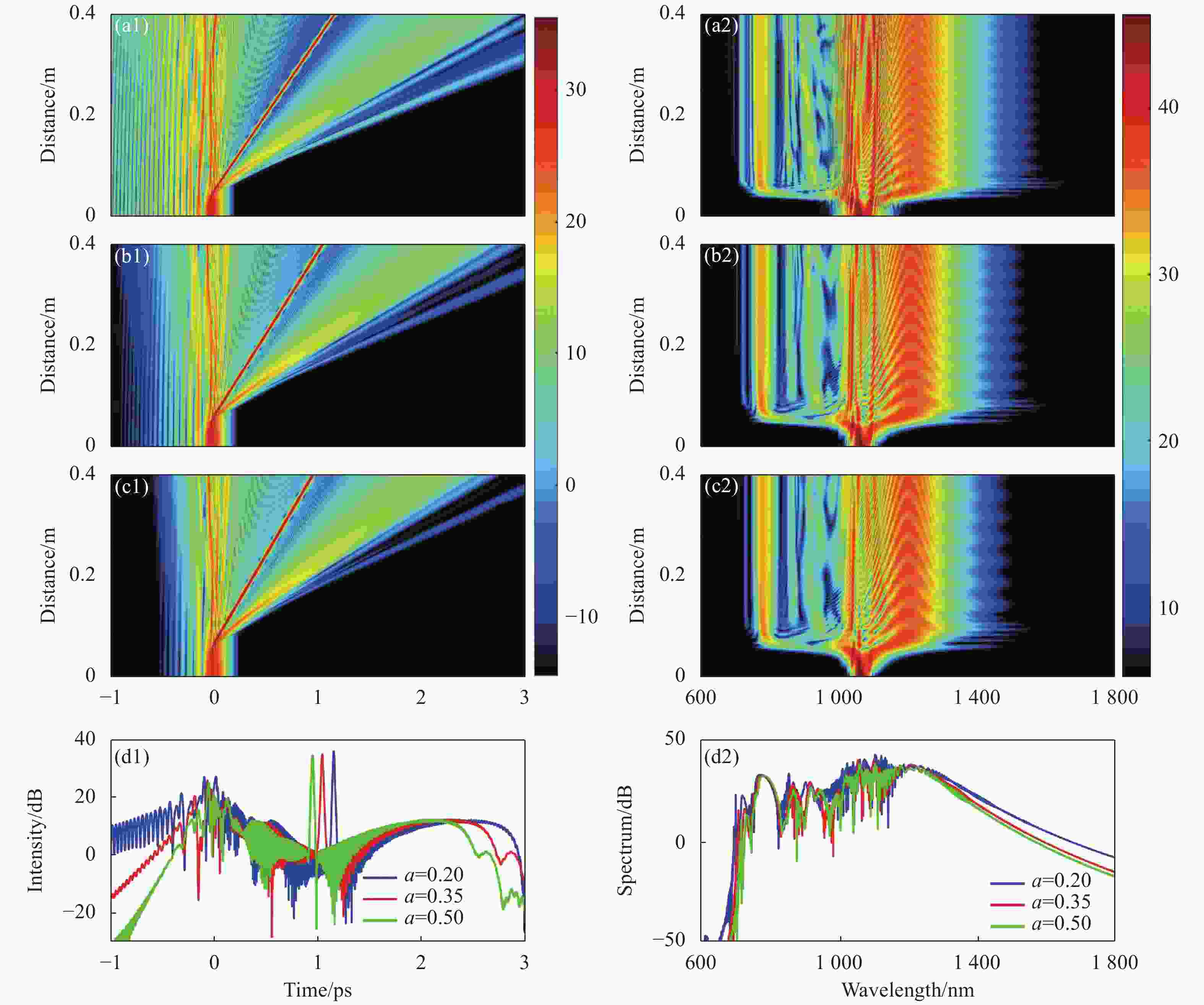
图 4 当P0=5 kW,C=0,χ0=0.15时,不同截断系数a的cosh-Airy脉冲在双零色散介质中的时域和频域演化情况。其中,(a1)~(a2) a=0.2,(b1)~(b2) a=0.35,(c1)~(c2) a=0.5,(d1)~(d2)表示传输距离为0.4 m时,截断系数分别为a=0.2(蓝线)、a=0.35(红线)、a=0.5(绿线)时所对应的波形与频谱图
Figure 4. For P0=5 kW, C=0 and χ0=0.15, temporal and spectral evolutions of cosh-Airy pulses with different truncation coefficient propagated in a double-zero dispersion media. (a1)-(a2) a=0.2, (c1)-(c2) a=0.35, (d1)-(d2) a=0.5, (d1)-(d2) at propagation distance z =0.4 m, the corresponding waveform and spectrum distributions for a=0.2 (blue line), a=0.35 (red line) and a=0.5 (green line)
初始啁啾C是控制cosh-Airy脉冲频谱的一个自由度,因此为了探究初始啁啾对cosh-Airy脉冲产生超连续谱的影响,进行了数值模拟研究。当P0=5 kW,a=0.1,χ0=0.03时,图5所示为具有不同初始啁啾的cosh-Airy脉冲在双零色散介质中的时域和频域演化情况。由图5可知,初始啁啾C能够导致cosh-Airy脉冲的频谱产生一个前沿或者后沿震荡结构。从时域演化图来看(图5(a1)~(c1)):初始啁啾并不能影响cosh-Airy脉冲的初始波形。但是随着传输距离的增加,负啁啾导致cosh-Airy脉冲的旁瓣群速度增加,在时域中表现为波形被拉长(图5 (a1))。而正啁啾则导致旁瓣速度降低,在时域中表现为波形被压缩(图5 (c1))。正啁啾导致cosh-Airy脉冲主峰所产生的孤子偏转角度减小,而负啁啾导致cosh-Airy脉冲主峰所产生的孤子偏转角度增大。从频域演化图来看:初始啁啾影响cosh-Airy脉冲的初始频谱结构,当C=0时,cosh-Airy脉冲的初始频谱是一个对称分布在中心波长处的钟型结构(图5 (c2))。负啁啾则是把中心能量转移到短波长侧,形成后拖尾(图5 (a2))。而正啁啾会将中心波长处的频谱能量转移到了长波长侧形成前振荡拖尾(图5 (c2))。啁啾的绝对值越大,形成的拖尾的长度越长。负啁啾导致能量转移到短波长侧,并不能导致色散波的宽度的增加但是填补了色散波与中央高阶孤子的坍塌结构,提高了超连续谱的平坦性。正啁啾导致能量转移到长波长侧,导致超连续谱的长波长侧的宽度急剧增加。初始啁啾能够让频谱展宽到数千纳米的波长,但是产生的超连续平坦性很差,严重影响产生的超连续谱的可用性,故初始啁啾的取值不能太大。

图 5 当P0=5 kW,a=0.1,χ0=0.03时,不同初始啁啾C的cosh-Airy脉冲在双零色散介质中的时域和频域演化情况。其中,(a1)~(a2) C=−0.3,(b1)~(b2) C=0,(c1)~(c2) C=0.3;(d1)~(d2)表示传输距离为0.4 m时,初始啁啾分别为C=−0.3 (蓝线)、C=0(红线)、C=0.3 (绿线)时所对应的波形与频谱图
Figure 5. For P0=5 kW, a=0.1 and χ0=0.03, temporal and spectral evolutions of cosh-Airy pulses with different initial chirp propagate in a double-zero dispersion media. (a1)-(a2) C=−0.3, (b1)-(b2) C=0, (c1)-(c2) C=0.3; (d1)-(d2) at propagation distance z =0.4 m, the corresponding waveform and spectrum distributions for C=−0.3 (blue line), C=0 (red line) and C=0.3 (green line)
分布因子χ0是控制cosh-Airy脉冲的波形的另一个自由度,为了探究分布因子对cosh-Airy脉冲产生超连续谱的影响,展开了数值模拟研究。当P0=5 kW,a=0.5,C=0时,不同分布因子的cosh-Airy脉冲在双零色散介质中的时域和频域演化情况如图6所示。从时域演化图来看(图6(b1)~(d1)):Airy脉冲为多峰结构,分布因子χ0能够控制旁瓣的能量大小。χ0为0.05时,Airy脉冲有少量振荡拖尾的旁瓣(图6(a1));当χ0增大时,脉冲振荡拖尾部分的旁瓣迅速增加,而脉冲总能量不变,即拖尾旁瓣能量转移到了旁瓣(图6(b1)~(c1))。cosh-Airy脉冲在双零色散介质中传输,受到高阶色散和Kerr非线性效应的共同作用。对于分布因子更大的cosh-Airy脉冲,由于其主峰的能量占比更小,其受到的非线性效应更小,高阶色散对主峰产生的高阶孤子的偏转效应就更大。从频域演化图来看,当截断系数χ0为0.05时,cosh-Airy脉冲所产生的超连续谱的宽度稳定在608 nm (图6(a2))。随着分布因子的增加,所产生的超连续谱的宽度发生了变化(图6(b2)~(c2))。特别值得注意的是:随着分布因子的增加,cosh-Airy脉冲在双零色散介质中产生的超连续谱的宽度并不是单调增加。通过以上分析可知,发现可以通过选取合适的分布因子,使得cosh-Airy脉冲产生超连续谱的宽度达到最大。
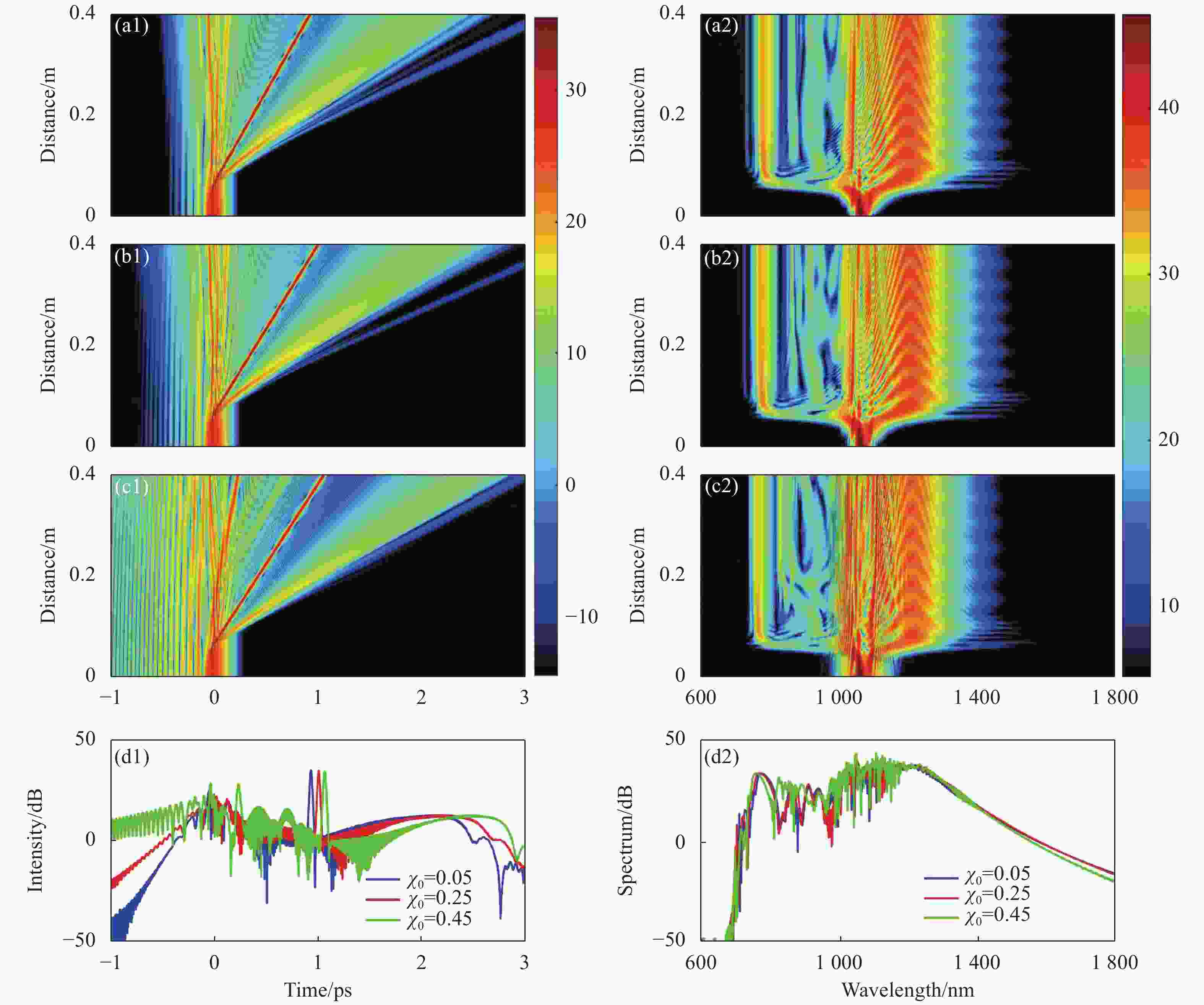
图 6 当P0=5 kW,a=0.5,C=0时,不同分布因子χ0的cosh-Airy脉冲在双零色散介质中的时域和频域演化情况。其中,(a1)~(a2) χ0=0.05,(b1)~(b2) χ0=0.25,(c1)~(c2) χ0=0.45;(d1)~(d2)表示传输距离为0.4 m时,分布因子分别为χ0=0.05 (蓝线)、χ0=0.25(红线)、χ0=0.45 (绿线)时所对应的波形与频谱图
Figure 6. For P0=5 kW, a=0.5 and C=0, temporal and spectral evolutions of cosh-Airy pulses with different sectional factor propagated in a double-zero dispersion media. (a1)-(a2) χ0=0.05, (b1)-(b2) χ0=0.25, (c1)-(c2) χ0=0.45; (d1)-(d2) at propagation distance z =0.4 m, the corresponding waveform and spectrum distributions for χ0=0.05 (blue line), χ0=0.25 (red line) and χ0=0.45 (green line)
图7对双零色散介质中不同截断系数、初始啁啾和分布因子对超连续谱宽度的影响进行统计。计算超连续谱的宽度采用以下公式:
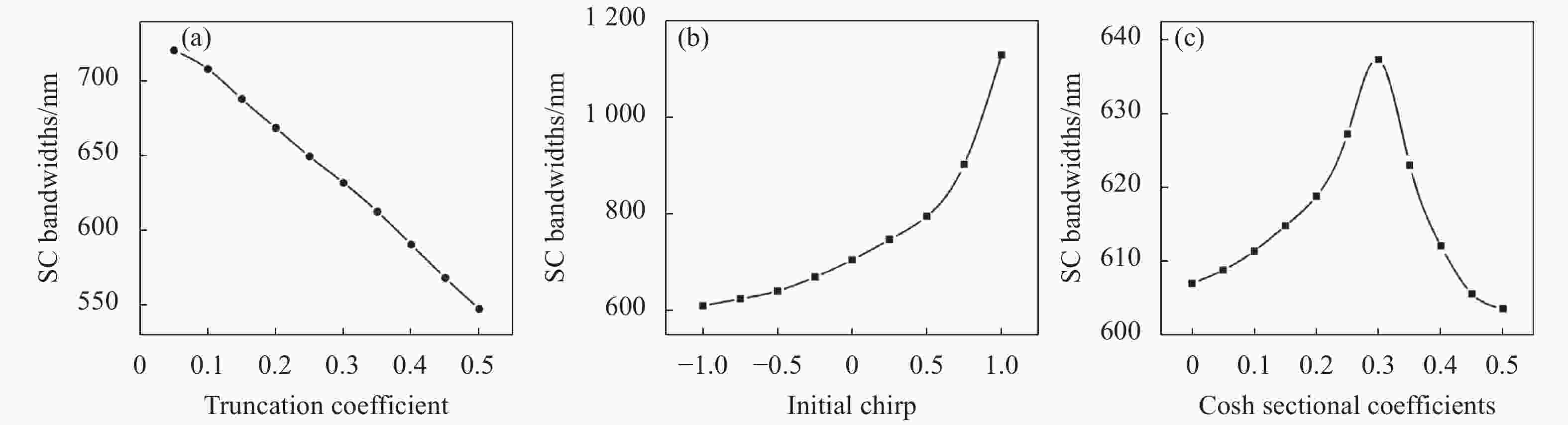
图 7 双零色散介质中,不同(a)截断系数、(b)初始啁啾和(c)分布因子对超连续谱宽度的影响
Figure 7. Effects of (a) truncation coefficient, (b) initial chirp and (c) sectional factor on the width of supercontinuum in double-zero dispersion media
$$ \sigma _u^2 = \left\langle {{{\left( {T - \left\langle T \right\rangle } \right)}^2}} \right\rangle = \frac{1}{{{P_0}}}{\int_{ - \infty }^{ + \infty } {{{\left( {T - \left\langle T \right\rangle } \right)}^2}\left| A \right|} ^2}{\rm{d}}T $$ (11) 式中:
$ \sigma _u^2 $ 表示均方根宽度。从cosh-Airy脉冲形成的超连续谱的宽度与其特征参数的关系图可以看出:超连续谱的宽度随截断系数的增加而近似单调递减(图7(a));负啁啾压缩超连续谱,正啁啾导致超连续谱宽度急剧增加,能够让频谱展宽到数千纳米的波长(图7(b));随着分布因子的增加,超连续谱先变宽,再变窄.表明存在一个最佳子脉冲间隔,使产生的超连续谱最宽(图7(c))。这对选择合适的双脉冲束缚态子脉冲间隔、优化超连续谱具有重要意义。cosh-Airy脉冲为两不同截断系数的Airy脉冲堆积而成。两Airy脉冲的四波混频的频谱发生相互作用产生新的频谱,位于斯托克斯方向,并远离原始色散波的频率,对超连续谱向长波长处的延伸起主导作用;堆积而成的cosh-Airy脉冲的四波混频与色散波相互作用产生的新频率则位于反斯托克斯方向,接近原始色散波的频率,有助于超连续谱向短波长处的延伸。值得注意的是,当χ0小于0.3时,子脉冲的截断系数为a+和a-。随着分布因子χ0的增大,a-的截断系数将会变小,截断系数为a-的Airy脉冲将具有更大的旁瓣而导致所产生的超连续谱增加。此时截断系数为a-的Airy脉冲对超连续其更大的作用。当分布因子大于0.3时,由于两Airy脉冲的截断系数的差别很大,子脉冲之间的四波混频、色散波之间的相互作用将越来越小,产生的超连续谱也将会越来越窄。
对于T0< 100 fs和P0>1 kW的飞秒脉冲,即使传输距离小于1 m,高阶非线性效应(受激拉曼效应和自陡峭)对超连续谱的影响也不可以忽略,因此有必要考虑高阶非线性效应对cosh-Airy脉冲产生超连续谱的影响。当P0=5 kW,a=0.5,χ0=0.45,C=0时,图8所示为cosh-Airy脉冲在不同非线性作用下的时域和频域演化情况。根据图8可以发现:当同时存在自相位调制和受激拉曼效应时,cosh-Airy脉冲在时域所脱落的孤子出现了自加速、自弯曲现象;频谱由于受激拉曼效应的影响出现往长波长方向(红移)显著移动,但是其蓝移部分的频率基本上保持不变,受激拉曼效应导致长波长部分延迟而短波长部分保持不变,导致频域出现一个非对称的坍塌结构。当同时存在自相位调制、受激拉曼效应和自陡效应时,自陡效应抑制了拉曼红移,减小了坍塌现象,对超连续谱的平坦性有巨大的提高。

图 8 当P0=5 kW,a=0.5,χ0=0.45,C=0时,cosh-Airy脉冲在不同非线性作用下的时域和频域演化图:(a1)~(a2) 只考虑自相位调制,(b1)~(b2) 同时考虑自相位调制和受激拉曼效应,(c1)~(c2) 同时考虑自相位调制、受激拉曼效应和自陡效应
Figure 8. For P0=5 kW, a=0.5, χ0=0.45 and C=0, temporal and spectral evolutions of cosh-Airy pulses propagate in double zero dispersion medium at different conditions: (a1)-(a2) self-phase modulation, (b1)-(b2) self-phase modulation and stimulated Raman scattering, (c1)-(c2) self-phase modulation, stimulated Raman scattering and self-steepening
-
通过改变双零色散介质中cosh-Airy脉冲的初始参数,可以获得宽度不同的超连续谱。因此合理地选择初始参数,以获得更高宽度的超连续谱是非常重要的。首先,详细分析了cosh-Airy脉冲在不同截断系数、初始啁啾和分布因子时的时域和频率演化特性;然后进一步分析了高阶非线性效应对cosh-Airy脉冲产生超连续谱的影响。结果表明:截断系数越小和正初始啁啾越大可以获得宽度更大的超连续谱,随着分布因子逐渐增加,超连续谱先变宽,再变窄,最后基本保持不变。受激拉曼效应能够使长波长频谱出现红移分量,导致频谱产生了坍塌结构。自陡效应能够抑制拉曼红移,减小了坍塌现象,对超连续谱的平坦性有巨大的提高。研究结果为超连续谱的产生与操控以及宽带激光光源提供了一些理论依据与参考。
Supercontinuum generation and manipulation of cosh-Airy pulse in double-zero dispersion medium
-
摘要: 结合分步傅里叶方法和四阶Runge-Kutta积分法,研究了有限能量cosh-Airy脉冲在双零色散介质中的超连续谱产生与操控。首先,详细讨论了特征参数截断系数a、初始啁啾C和分布因子χ0对cosh-Airy脉冲在双零色散介质中的演化影响,并统计了a、C和χ0对超连续谱宽度的影响。然后,进一步研究了高阶非线性效应对cosh-Airy脉冲产生超连续谱的影响。结果表明:通过操控cosh-Airy脉冲的特征参数可以控制超连续谱的宽度;当存在高阶非线性效应时,超连续谱的平坦性会受到影响。研究结果为超连续谱的产生和操控以及宽带激光光源提供一些理论基础。
-
关键词:
- cosh-Airy脉冲 /
- 双零色散介质 /
- 超连续谱 /
- 操控
Abstract: Combining the split-step Fourier method with the fourth-order Runge-Kutta integration method, the manipulation and generation of supercontinuum by finite energy cosh-Airy pulses in a double-zero dispersion media was investigated. Firstly, the influences of truncation coefficient a, initial chirp C and distribution factor χ0 on the evolution of cosh-Airy pulses in double-zero dispersion medium were discussed in detail, and the influences of a, C and χ0 on the width of supercontinuum width were statistically analyzed. Then, the influences of higher-order nonlinear effects on supercontinuum generation of cosh-Airy pulse was further studied. The results show that the width of supercontinuum can be controlled by manipulating the characteristic parameters of cosh-Airy pulses. The flatness of supercontinuum is affected with consideration of high-order nonlinear effects. The results provide some theoretical basis for manipulation and generation of supercontinuum and broadband laser sources.-
Key words:
- cosh-Airy pulse /
- double-zero dispersion medium /
- supercontinuum /
- manipulation
-
图 4 当P0=5 kW,C=0,χ0=0.15时,不同截断系数a的cosh-Airy脉冲在双零色散介质中的时域和频域演化情况。其中,(a1)~(a2) a=0.2,(b1)~(b2) a=0.35,(c1)~(c2) a=0.5,(d1)~(d2)表示传输距离为0.4 m时,截断系数分别为a=0.2(蓝线)、a=0.35(红线)、a=0.5(绿线)时所对应的波形与频谱图
Figure 4. For P0=5 kW, C=0 and χ0=0.15, temporal and spectral evolutions of cosh-Airy pulses with different truncation coefficient propagated in a double-zero dispersion media. (a1)-(a2) a=0.2, (c1)-(c2) a=0.35, (d1)-(d2) a=0.5, (d1)-(d2) at propagation distance z =0.4 m, the corresponding waveform and spectrum distributions for a=0.2 (blue line), a=0.35 (red line) and a=0.5 (green line)
图 5 当P0=5 kW,a=0.1,χ0=0.03时,不同初始啁啾C的cosh-Airy脉冲在双零色散介质中的时域和频域演化情况。其中,(a1)~(a2) C=−0.3,(b1)~(b2) C=0,(c1)~(c2) C=0.3;(d1)~(d2)表示传输距离为0.4 m时,初始啁啾分别为C=−0.3 (蓝线)、C=0(红线)、C=0.3 (绿线)时所对应的波形与频谱图
Figure 5. For P0=5 kW, a=0.1 and χ0=0.03, temporal and spectral evolutions of cosh-Airy pulses with different initial chirp propagate in a double-zero dispersion media. (a1)-(a2) C=−0.3, (b1)-(b2) C=0, (c1)-(c2) C=0.3; (d1)-(d2) at propagation distance z =0.4 m, the corresponding waveform and spectrum distributions for C=−0.3 (blue line), C=0 (red line) and C=0.3 (green line)
图 6 当P0=5 kW,a=0.5,C=0时,不同分布因子χ0的cosh-Airy脉冲在双零色散介质中的时域和频域演化情况。其中,(a1)~(a2) χ0=0.05,(b1)~(b2) χ0=0.25,(c1)~(c2) χ0=0.45;(d1)~(d2)表示传输距离为0.4 m时,分布因子分别为χ0=0.05 (蓝线)、χ0=0.25(红线)、χ0=0.45 (绿线)时所对应的波形与频谱图
Figure 6. For P0=5 kW, a=0.5 and C=0, temporal and spectral evolutions of cosh-Airy pulses with different sectional factor propagated in a double-zero dispersion media. (a1)-(a2) χ0=0.05, (b1)-(b2) χ0=0.25, (c1)-(c2) χ0=0.45; (d1)-(d2) at propagation distance z =0.4 m, the corresponding waveform and spectrum distributions for χ0=0.05 (blue line), χ0=0.25 (red line) and χ0=0.45 (green line)
图 8 当P0=5 kW,a=0.5,χ0=0.45,C=0时,cosh-Airy脉冲在不同非线性作用下的时域和频域演化图:(a1)~(a2) 只考虑自相位调制,(b1)~(b2) 同时考虑自相位调制和受激拉曼效应,(c1)~(c2) 同时考虑自相位调制、受激拉曼效应和自陡效应
Figure 8. For P0=5 kW, a=0.5, χ0=0.45 and C=0, temporal and spectral evolutions of cosh-Airy pulses propagate in double zero dispersion medium at different conditions: (a1)-(a2) self-phase modulation, (b1)-(b2) self-phase modulation and stimulated Raman scattering, (c1)-(c2) self-phase modulation, stimulated Raman scattering and self-steepening
-
[1] Alfano R R, Shapiro S L. Emission in the region 4000 to 7000 Å via four-photon coupling in glass [J]. Phys Rev Lett, 1970, 24: 584-587. doi: 10.1103/PhysRevLett.24.584 [2] Alfano R R, Shapiro S L. Observation of self-phase modulation and small-scale filaments in crystals and glasses [J]. Phys Rev Lett, 1970, 24: 592-594. doi: 10.1103/PhysRevLett.24.592 [3] Marks D L, Oldenburg A L, Reynolds J J, et al. Study of an ultrahigh-numerical-aperture fiber continuum generation source for optical coherence tomography [J]. Opt Lett, 2002, 27(22): 2010-2012. doi: 10.1364/OL.27.002010 [4] Ruehl A, Martin M J, Cossel K C, et al. Ultrabroadband coherent supercontinuum frequency comb [J]. Phys Rev A, 2011, 84: 011806. doi: 10.1103/PhysRevA.84.011806 [5] Maria M, Gonzalo I B, Feuchter T, et al. Q-switch-pumped supercontinuum for ultra-high resolution optical coherence tomography [J]. Opt Letters, 2017, 42(22): 4744-4747. doi: 10.1364/OL.42.004744 [6] Smirnov S V, Ania-Castanon J D, Ellingham T J, et al. Optical spectral broadening and supercontinuum generation in telecom applications [J]. Opt Fiber Technol, 2006, 12(2): 122-147. doi: 10.1016/j.yofte.2005.07.004 [7] Wakayama T, Takahashi Y, Ono Y, et al. Three-dimensional measurement of an inner surface profile using a supercontinuum beam [J]. App Optics, 2018, 57(19): 5371-5379. doi: 10.1364/AO.57.005371 [8] Akhmediev N, Karlsson M. Cherenkov radiation emitted by solitons in optical fibers [J]. Phys Rev A, 1995, 51: 2602-2607. doi: 10.1103/PhysRevA.51.2602 [9] Chang G Q, Chen L J, Kärtner F X. Highly efficient Cherenkov radiation in photonic crystal fibers for broadband visible wavelength generation [J]. Opt Lett, 2010, 35(14): 2361-2363. doi: 10.1364/OL.35.002361 [10] Milián C, Ferrando A, Skryabin D V. Polychromatic Cherenkov radiation and supercontinuum in tapered optical fibers [J]. J Opt Soc Am B, 2012, 29(4): 589-593. doi: 10.1364/JOSAB.29.000589 [11] Husakou A V, Herrmann J. Supercontinuum generation of higher-order solitons by fission in photonic crystal fibers [J]. Phys Rev Lett, 2001, 87(20): 203901. doi: 10.1103/PhysRevLett.87.203901 [12] Qi X, Chen S, Li Z, et al. High-power visible-enhanced all-fiber supercontinuum generation in a seven-core photonic crystal fiber pumped at 1016 nm [J]. Opt Lett, 2018, 43(5): 1019-1022. doi: 10.1364/OL.43.001019 [13] Zhao S, Yang H, Zhao C, et al. Harnessing rogue wave for supercontinuum generation in cascaded photonic crystal fiber [J]. Opt Exp, 2017, 25(7): 7192. doi: 10.1364/OE.25.007192 [14] Wang J Y, Jiang C, Hu W S, et al. Modified design of photonic crystal fibers with flattened dispersion [J]. Optics and Laser Technology, 2006, 38(3): 169-172. doi: 10.1016/j.optlastec.2004.11.016 [15] Bandres M A, Rodriguezlara B M. Nondiffracting accelerating waves: weber waves and parabolic momentum [J]. New J Phys, 2013, 15: 013054. doi: 10.1088/1367-2630/15/1/013054 [16] Aleahmad P, Miri M A, Mills M S, et al. Fully vectorial accelerating diffraction-free Helmholtz beams [J]. Phys Rev Lett, 2012, 109: 203902. doi: 10.1103/PhysRevLett.109.203902 [17] Ament C, Polynkin P, Moloney J V. Supercontinuum generation with femtosecond self-healing Airy pulses [J]. Phys Rev Lett, 2011, 107: 243901. doi: 10.1103/PhysRevLett.107.243901 [18] Zhang L F, Zhang J G, Chen Y, et al. Dynamic propagation of finite-energy Airy pulses in the presence of higher-order effects [J]. J Opt Soc Am B, 2014, 31(4): 889-897. doi: 10.1364/JOSAB.31.000889 [19] Zhang L F, Zhong H Z. Modulation instability of finite energy Airy pulse in optical fiber [J]. Opt Express, 2014, 22(14): 17107-17115. doi: 10.1364/OE.22.017107 [20] Baumgartl J, Mazilu M, Dholakia K. Optically mediated particle clearing using Airy wavepackets [J]. Nat Photonics, 2008, 2: 675-678. doi: 10.1038/nphoton.2008.201 [21] Polynkin P, Kolesik M, Moloney J V, et al. Curved plasma channel generation using ultra intense Airy beams [J]. Science, 2009, 324: 229-232. doi: 10.1126/science.1169544 [22] Ellenbogen T, Voloch-Bloch N, Ganany P A, et al. Nonlinear generation and manipulation of Airy beams [J]. Nat Photonics, 2009, 3: 395-398. doi: 10.1038/nphoton.2009.95 [23] Jia S, Lee J, Fleischer J W, et al. Diffusion-trapped airy beams in photorefractive media [J]. Phys Rev Lett, 2010, 104: 253904-253907. doi: 10.1103/PhysRevLett.104.253904 [24] Rose P, Diebel F, Boguslawski M, et al. Airy beam induced optical routing [J]. Appl Phys Lett, 2013, 102: 101101-101103. doi: 10.1063/1.4793668 [25] Li H H, Wang J G, Tang M M, et al. Propagation properties of cosh-Airy beams [J]. J Mod Opt, 2018, 65(3): 314-320. doi: 10.1080/09500340.2017.1393572 [26] Ouahid L, Dalil E L, Belafhal A. Effect of light absorption and temperature on self-focusing of finite airy Gaussian beams in plasma with relativistic and ponderomotive regime [J]. Quantum Electron, 2018, 50: 216-232. doi: 10.1007/s11082-018-1483-3 [27] Zhou Y M, Xu Y Q, Chu X X, et al. Propagation of cosh-Airy and Cos-Airy beams in parabolic potential [J]. Appl Sci, 2019, 9(24): 5530. doi: 10.3390/app9245530 [28] Zhou G Q, Chen R P, Chu X X. Propagation of cosh-Airy beams in uniaxial crystals orthogonal to the optical axis [J]. Opt Laser Technol, 2019, 116: 72-82. doi: 10.1016/j.optlastec.2019.03.016 [29] Zhou G Q, Chu X X, Chen R P, et al. Self-healing properties of cosh-Airy beams [J]. Laser Phys, 2019, 29(2): 025001. doi: 10.1088/1555-6611/aaf641 [30] Tiofack C G L, Ndzana F I, Mohamadou A, et al. Spatial solitons and stability in the one-dimensional and the two-dimensional generalized nonlinear Schrödinger equation with fourth-order diffraction and parity-time-symmetric potentials [J]. Phys Rev E, 2018, 97(3): 032204. doi: 10.1103/PhysRevE.97.032204 [31] Wen J, Liu H, Huang N, et al. Influence of the initial chirp on the supercontinuum generation in silicon-on-insulator waveguide [J]. Appl Phys B, 2011, 104: 867-871. doi: 10.1007/s00340-011-4496-1 [32] Saitoh K, Koshiba M. Empirical relations for simple design of photonic crystal fibers [J]. Opt Exp, 2005, 13(1): 267-274. doi: 10.1364/OPEX.13.000267 [33] Jiang L H, Hou L T. Effect of structure parameters changes on the properties of photonic crystal fiber with two zero-dispersion wavelengths [J]. Acta Phys Sin, 2010, 59: 1095-1100. -






 下载:
下载: