-
非球面光学元件以其多自由度的特点，能够校正像差，提升像质，同时减小光学系统的尺寸与质量，已经广泛应用于多种光学系统之中。在反射式光学系统中，通常次镜会采用凸非球面，因此凸非球面的高精度加工和检测也成为光学制造领域的热点。而面形检测精度作为补偿修正加工的基础和依据，凸非球面的高精度面形检测显得尤为重要。常用的凸非球面面形高精度检测技术包括逆向哈特曼检测技术[1-2]、子孔径拼接干涉检测技术[3-5]和零位干涉补偿检测技术[6-13]等。
逆向哈特曼检测技术是对哈特曼检测光路的逆向使用，通过精确标定被测镜、显示屏（LCD）和探测器（CCD）之间的位置关系，对被测镜的斜率数据进行积分重构，从而计算得到其面形误差。2020年，Shanshan Wang等人[1]采用该技术对一口径为80 mm的凸非球面进行了测量，检测结果峰谷值（Peak to Valley, PV）为278.93 nm，与直接的干涉仪检测结果非常吻合。
子孔径拼接检测法是将凸非球面反射镜分成若干子孔径，分别采用干涉检测，然后通过拼接算法获得全口径面形信息，该方法虽然无需任何辅助补偿元件，但其测量效率偏低，且拼接算法不统一，测量误差和拼接算法误差都会影响检测精度。2021年，蔡志华等人[5]采用非零位子孔径拼接技术实现了对口径为120 mm的凸双曲面金属反射镜的测量，检测结果均方根值（Root Mean Square, RMS）为0.016λ。
Hindle球检测法[6-7]是检测凸二次非球面的经典零位干涉检测方法。该方法因其具有设计简单、检验精度高等优点经常被采用，但该方法存在中心遮拦且对球差不敏感，同时，大口径的辅助球面的制造和装调难度的限制使该方法存在一定的局限性。2019年，赵鹏玮等人[6]基于Hindle球检测法，提出了一种小口径透镜与球面反射镜组合检测大口径凸非球面的方法，有效地减小了辅助球面反射镜的口径，缩短了检测光路的长度，并完成了对某口径为800 mm的凸双曲面的检测光路设计。为了克服Hindle球检测法的缺陷，改进的Hindle法[8-9]能较好地解决经典Hindle球检验方法中辅助球面镜口径过大导致的装调以及选材和加工困难等问题，但该方法需要一个弯月透镜作为辅助元件，且需要在其凸面上镀半反半透膜，这也是不小的难题。且该方法对被测凸非球面的反射率有较高的要求。2020年，戚丽丽等人[8]基于Simpson检测光路，提出了一种自准校正透镜凸面自准检验凸非球面的方法，并实现了对一口径为287 mm的凸非球面的面形检测，检测结果PV为0.474λ。
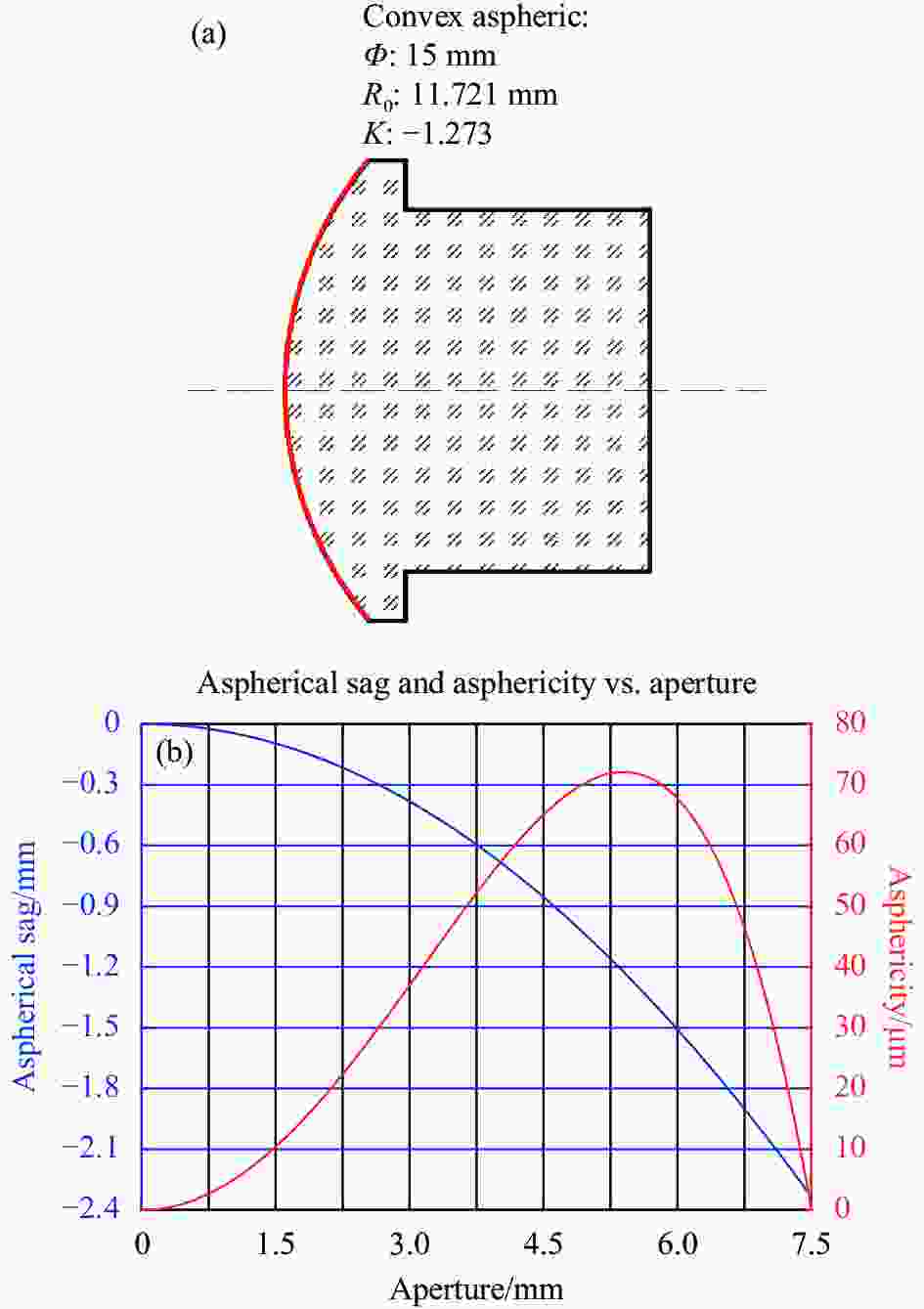
深度非球面都有较大的非球面度和非球面梯度，故在零位补偿干涉检测中需要补偿的像差较大，其对应的补偿元件的设计比较困难[14-15]。文中针对小口径深度凸非球面的高精度面形检测要求，采用基于计算全息图的零位干涉检测方法，并对其检测原理与设计方法进行了详细介绍分析。结合工程应用，对某口径D=15 mm，顶点曲率半径R=11.721 mm，圆锥系数K=–1.273的深度凸非球面，设计并制造了相应的CGH，实现了对面形的高精度检测，并交叉验证了其准确性。
-
为了对非球面的像差进行补偿，实现零位检测，一般采用基于补偿透镜的折射补偿原理或基于计算全息图（computer generated hologram, CGH）的衍射补偿原理。折射补偿原理需要设计并加工高精度的透射光学元件，称为补偿器，但补偿器的加工和标定，以及其在检测光路中的位姿情况均会对非球面的面形检测产生影响。衍射补偿原理是以可变间距光栅作为补偿元件，称为CGH，对衍射波前进行调制，以补偿非球面的像差。CGH采用光刻工艺进行加工，其精度能够得到保证，同时CGH上也都对准标记，能够实现检测系统的高精度对准，确保检测精度。
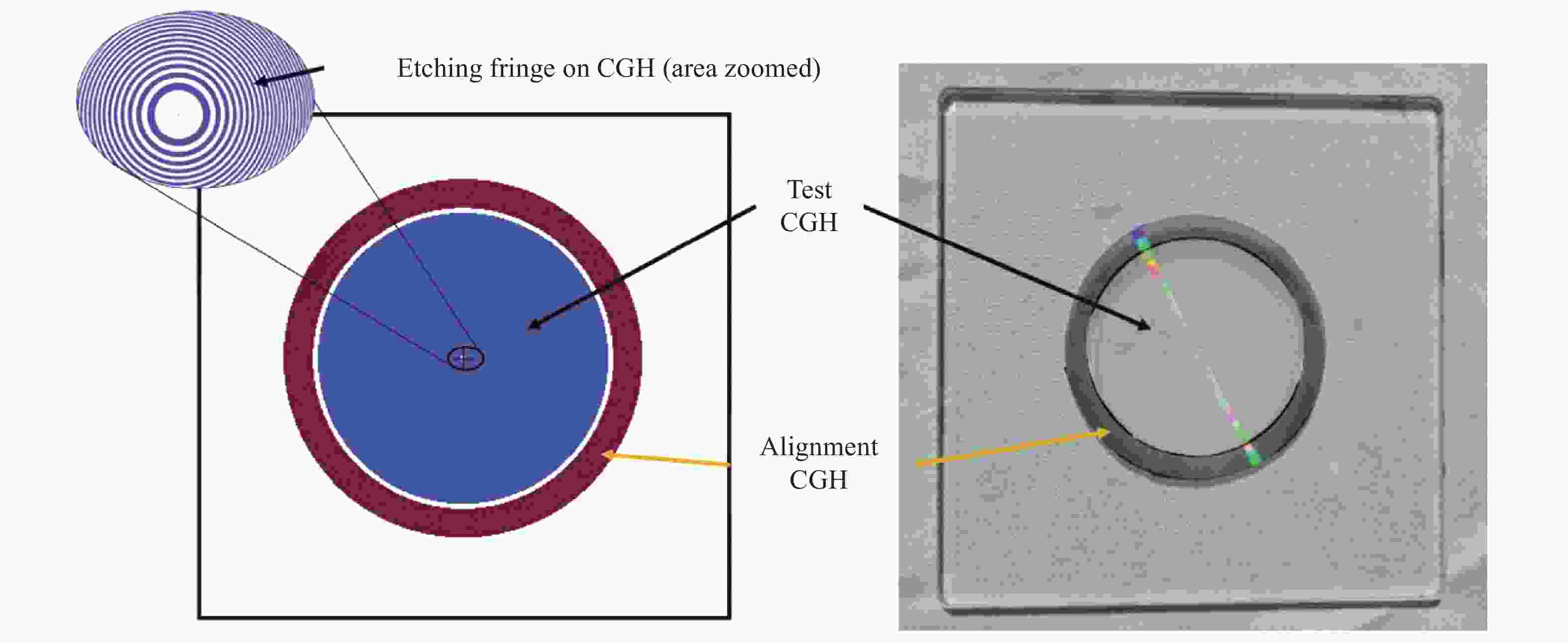
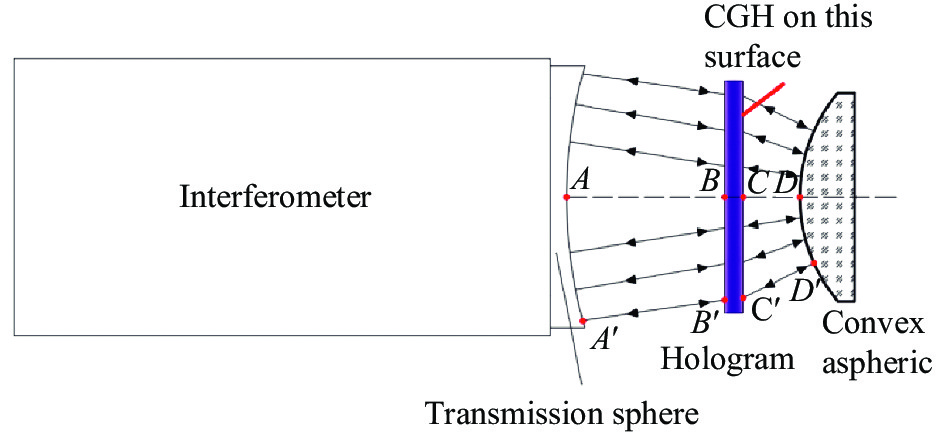
当采用CGH对凸非球面进行检测时，根据被测非球面参数的不同，选择合适的标准镜头，利用CGH衍射效应对波前形状进行调制，将波前变为标准的凸非球面波前，从而实现对凸非球面的零位检测。一般而言，CGH的中间部分为测试全息，用于补偿被测凸非球面的像差，实现零位检测；测试全息的外围部分为对准标记全息，实现检测系统中不同光学元件之间的对准，如干涉仪与CGH之间的对准，或CGH与被测非球面之间的对准。CGH法检测凸非球面的原理如图1所示。
图 1 CGH法检测凸非球面原理图
Figure 1. Schematic diagram of testing convex aspheric with CGH method
CGH设计最重要的是调制波前形状的设计，其由刻蚀条纹的位置和间距决定。可采用光线追迹法设计得到刻蚀条纹的相关信息。在设计测试全息时，需利用CGH衍射波前对凸非球面不同口径的像差进行补偿，根据标量衍射理论，CGH的相位函数应满足如下公式：
$$ \begin{split} \Delta Phase =& \frac{{2\pi }}{\lambda }[ {\left( {A'B' + n \cdot B'C' + C'D'} \right) }-\\ &{\left( {AB + n \cdot BC + CD} \right)} ] \end{split}$$ (1) 而在设计对准标记全息（用于干涉仪与全息片之间的对准）时，由于光线在CGH的刻蚀面发射反射衍射，故公式(1)应变为：
$$ \Delta Phase = \frac{{2\pi }}{\lambda }\left[ {\left( {A'B' + n\cdot B'C'} \right) - \left( {AB + n \cdot BC} \right)} \right] $$ (2) 式中：A、B、C、D为参考光线上的点；而A'、B'、C'、D'为任意口径上光线的点；n为CGH基片的折射率；λ为检测波长。利用上述公式，根据光线追迹算法计算得到CGH刻蚀面上各条纹的位置坐标，即可获得CGH的相位函数分布情况，然后对该相位函数进行编码，便可获得CGH的加工数据[16-17]。
在设计CGH时，除了需要考虑CGH的整体口径外，最重要是在保证系统补偿检测设计精度的同时，降低CGH的条纹刻线密度，降低其制造难度和成本，以确保CGH的制造精度。CGH条纹刻线密度与检测光路所需补偿的像差大小密切相关，而检测系统像差大小则与各元件的几何距离参数有关。故在设计过程中，需通过调整标准镜头、CGH、被测凸非球面之间的间距（即图1中AB与CD的距离），以确定检测光路所需补偿的像差，然后进行CGH设计（以CGH条纹刻线密度与CGH口径为约束反馈），通过不断的迭代优化，以获得最优设计结果。
CGH的设计除了需要设计CGH的条纹刻线位置，以保证其衍射波前的形状外，还需设计合适的衍射类型和衍射级次，以获得合理的衍射效率，保证干涉条纹的对比度。二元相位型CGH的衍射效率（一级衍射效率约为40%）比二元振幅型CGH（一级衍射效率约为10%）的高，常用于检测非球面的补偿测试全息，因为测试光需要两次通过测试全息，对光强的损失比较严重。类似地，CGH中也常选用低的衍射级次，因为随着衍射级次的增加，其衍射效率降低非常明显[18]。但对于对准标记全息而言，因为对准标记通常只需发生一次衍射，故相位型CGH或振幅型CGH的三级衍射级次，其衍射效率均已够用。同时，这也能有效降低条纹刻线密度，减小制造难度。
-
根据某反射系统的需要，其次镜为凸非球面，具体参数如图2(a)所示。根据该参数计算得到其最大矢高为2.336 mm，倾角达到31.25°，非球面度高达72 μm，是一个深度非球面。如图2（b）所示，该凸非球面的口径虽然较小，但其矢高与非球面度却很大，需要补偿的像差很大，由于是轴对称元件，故主要的像差为球差和高阶球差。
图 2 凸非球面参数与仿真结果。(a) 凸非球面参数；(b) 矢高与非球面度仿真结果
Figure 2. Convex aspheric parameters and simulation results. (a) Convex aspheric parameters; (b) Simulation results of vector height and asphericity
-
由于该被测凸非球面的相对孔径较大，结合实验室的4 in (1 in=2.54 cm)Zygo干涉仪，为了降低CGH的刻线密度，选用球面标准镜头对其进行检测，并以此设计相应的CGH，如图1所示。利用标准球面镜头的汇聚光路进行检测，很容易抑制鬼像，畸变小，CGH 线宽增加，容易加工。
根据CGH基片的定制加工结果，尺寸为101.6 mm×101.6 mm、厚度为4.97 mm的方形熔石英玻璃材料。为了实现对非球面镜的全口径测量，所设计的CGH检测口径需大于被测凸非球面的口径，同时，由于被测凸非球面的顶点曲率只有11.721 mm，受限于4 in干涉仪的口径，几乎只能选用F/1.5的球面标准镜头（参考面半径为121.2 mm，有效口径为81 mm）。因此标准镜头、CGH、被测面三者之间的距离很近，CGH位于该标准镜头的焦点之内，两者距离只有35 mm，而CGH与被测凸非球面之间的距离也只有20 mm，如图3所示。
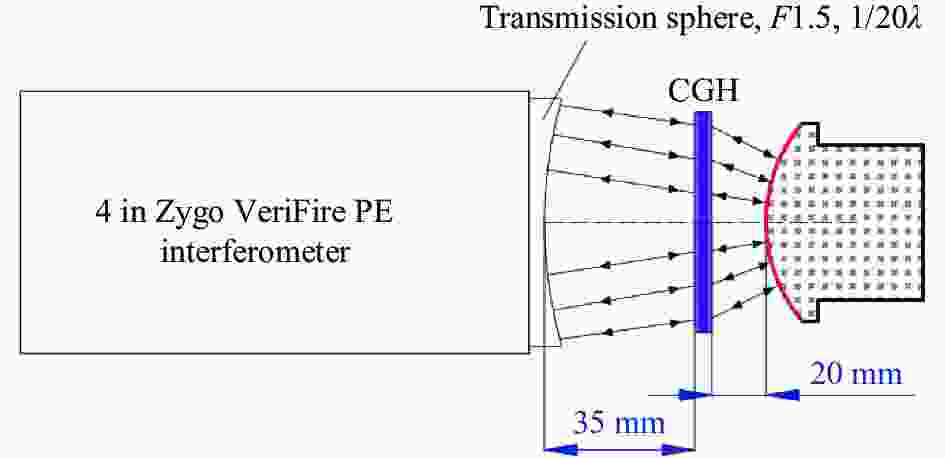
图 3 CGH检测凸非球面面形光路结构参数
Figure 3. Optical path structure parameters of convex aspheric detected by CGH
在ZEMAX中对上述检测光路进行了设计，采用Binary 2模拟CGH的条纹刻蚀面，选用+1级衍射级次，通过优化其各项的系数，得到的结果如图4所示。可以看出，通过优化设计，补偿测试全息的使用口径为42 mm，共包括5260个条纹，最大条纹周期为416 line/mm，最小条纹宽度约2.4 μm。该检测系统的理论剩余波前误差PV ≤0.0001λ，RMS ≤0.0001λ，如图4(a)所示，该理论误差可以忽略不计。测试全息设计完成后，对该CGH的其他衍射级次（主要包括–1级，±3级，±5级）进行分析，未发现鬼像影响。
图 4 补偿测试全息设计结果。(a) 剩余波前差；(b) CGH相位与条纹频率分布
Figure 4. Test CGH design results. (a) Residual wavefront; (b) CGH phase and fringe frequency distribution
-
当补偿测试全息设计完成后，检测光路中各元件之间的距离参数已经确定。该检测系统主要包括干涉仪、CGH和被测凸非球面三个元件，检测系统的对准包括干涉仪与CGH之间的对准和CGH与凸非球面之间的对准两个部分。此处所设计的对准标记全息用于干涉仪与CGH之间的对准，通过干涉条纹的对准标记，其对准精度可达到纳米量级。而CGH与凸非球面之间的对准，可以根据检测结果中引入误差的类似予以监控与调整。当CGH与凸非球面未处于完全对准时，为在干涉检测结果中引入离焦、慧差等像差，通过调节凸非球面的平移和倾斜，将这些误差调节至最小，即可使CGH与凸非球面处于完全对准状态。
对准标记全息的设计，可根据标准镜头与CGH之间的距离参数，在CGH的刻蚀面避开中间补偿测试全息所用的部分，优化对准标记全息的相位系数，获得其刻蚀条纹的相关信息，设计结果如图5所示。
图 5 对准标记全息设计结果。(a) 剩余波前差；(b) CGH相位与条纹频率分布
Figure 5. Alignment CGH design results. (a) Residual wavefront; (b) CGH phase and fringe frequency distribution
对准标记全息部分选用+3级衍射级次，其所用口径为43~50 mm部分，包括1282个条纹，最大条纹周期为328 line/mm，最小条纹宽度约3.0 μm。该对准全息部分的理论剩余波前误差PV ≤0.0001λ，RMS ≤0.0001λ，如图5(a)所示，该理论误差可以忽略不计。
-
由上述设计结果可知，该CGH由两部分组成，分别使用全息基片的不同部分，以实现不同的功能。CGH属于二元台阶型衍射光学元件，一般采用光刻或激光直写工艺进行加工。加工前，对CGH基板的加工精度进行严格控制，主要包括基片的厚度（误差≤±0.005 mm）和透射波前（误差RMS≤5 nm）。所用的CGH是采用光刻技术，首先制作掩膜板，掩膜板在电子束曝光系统中制作，然后将条纹图拷贝到 CGH 基板上。加工完后采用高精度台阶仪对二元台阶高度进行测量，要求台阶均匀性≤±5%，以确保CGH的制造精度和衍射效率。该CGH的整体设计与制造结果如表1和图6所示，其为间距可变的同心二元台阶结构。
表 1 CGH设计结果与制造参数
Table 1. CGH design result and its manufacturing parameter
Parameters Test CGH Alignment CGH Manufacturing error CGH substrate material Corning 7980 - CGH substrate size 101.6 mm×101.6 mm×4.970 mm Thickness error: 0.002 mm
Transmission wavefront (RMS): 4.98 nmDiffraction type Phase Amplitude - Diffraction order +1 +3 - Width ratio 0.5 - Step height 460 nm - Step uniformity: 1.3% Aperture range 0-42 mm 43-50 mm - Fringe number 5260 1282 - Minimum fringe width About 2.4 μm About 3.0 μm - 
图 6 CGH设计仿真图与加工实物
Figure 6. Diagram of CGH design simulation and processing object
-
CGH制作完成后，按照如图3所示的检测光路设计结果搭建面形检测光路，测试现场如图7(a)所示。首先调节CGH与干涉仪标准镜头之间的对准，利用对准标记全息，通过调节CGH使对准标记全息干涉条纹调节至零条纹，确保两者处于精确对准状态。然后将被测凸非球面放置在光路大致位置，根据干涉条纹情况逐步调整被测凸非球面的位姿，直至将离焦、彗差等调整误差调节到可忽略不计时，此时凸非球面与CGH也处于完全对准状态，其测量得到的结果即为被测凸非球面的面形误差。测试结果如图7(b)所示，PV为251.05 nm，RMS为54.376 nm，从检测结果可以看出，检测过程不存在其他衍射级次的干扰，同时该元件表面存在较大的球差。
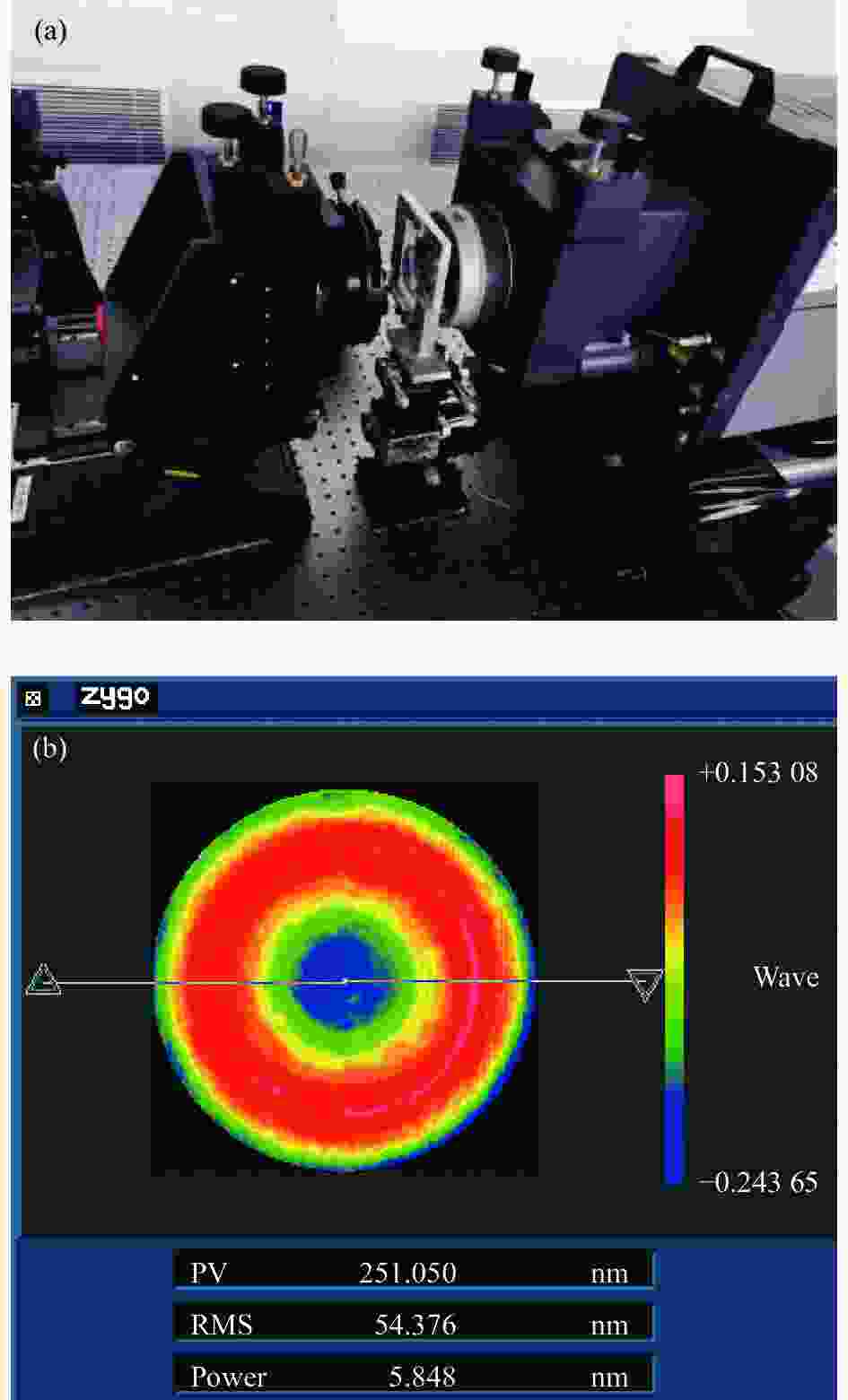
图 7 CGH法测量凸非球面。(a) 检测现场；(b) 面形检测结果
Figure 7. Measurement of convex aspheric by CGH method. (a) Test site; (b) Test result of surface shape
为了验证计算全息法的检测结果，采用 Taylor Hobson公司的Luphoscan非接触轮廓仪对该凸非球面镜进行检测，检测现场与测试结果如图8所示，PV为235 nm，RMS为55 nm。
图 8 Luphoscan法测量凸非球面。(a) 检测现场；(b) 面形检测结果
Figure 8. Measurement of convex aspheric by Luphoscan method. (a) Test site; (b) Surface shape test results
对比该凸非球面的CGH法和Luphoscan法的测量结果，从图7和图8可以看到，不同方法检测结果的面形PV和RMS都非常接近，其面形分布情况也非常类似，呈现的主要误差为球差，为被测凸非球面表面的实际误差。
由于CGH检测法在设计阶段和CGH制造阶段的误差都能得到保证，同时在检测光路调节中可利用对准标记全息保证各元件之间的实际位置关系进行精确标定，故其检测结果的准确性能够得到保证。另外，Luphoscan非接触轮廓扫描法在检测过程中不需要其他附加元件，其检测结果也具有很高的可信度。这两种方法检测结果的高度一致性，也能确保被测凸非球面面形检测结果的准确性。
-
文中针对小口径深度凸非球面的高精度面形检测需求，提出基于CGH的零位干涉检测方法，对其检测原理及设计过程的关键点进行了详细阐述。CGH检测法的设计精度和制造精度的可靠性，以及检测光路调节过程的实际位置精度的可监控性，能够确保检测结果的准确性，使得该方法具有广泛的应用前景。针对口径为15 mm、顶点曲率半径为11.721 mm、圆锥系数为–1.273的深度凸非球面进行了详细的CGH检测光路设计，制造了相应的CGH，完成了面形检测实验。其检测结果与Luphoscan非接触轮廓仪测量结果具有高度一致性，交叉验证了CGH设计方法的正确性与面形检测结果的可靠性。为该类元件的高精度制造提供了有效的技术保障。
High-precision shape measurement technology for convex aspheric with small aperture and large convex asphericity
-
摘要: 凸非球面反射镜在反射式光学系统中的应用非常广泛，但其面形高精度检测一直是光学制造领域的难题。为了实现小口径、深度凸非球面的面形高精度检测，提出了一种基于计算全息图（Computer Generated Hologram，CGH）的零位干涉检测技术。首先，详细阐述了该技术的检测原理和方法，给出了计算全息中补偿测试全息和对准标记全息设计过程中的技术要点；然后结合工程应用，针对口径15 mm、顶点曲率半径11.721 mm、非球面度达到72 μm的深度凸非球面，设计并制造了相应的CGH补偿元件，完成了相应零位干涉检测系统的搭建和检测实验；最后，与Luphoscan的检测结果交叉对比，验证了该检测方法的准确性。该技术为小口径凸非球面的高精度检测提供了一种有效的方法，具有显著的工程应用价值。Abstract: Convex aspherical mirrors are widely used in reflective optical systems, but high-precision shape measurement technology is always a difficult problem in optical manufacturing. In order to achieve high- precision detection of convex aspheric with small aperture and large asphericity, a null test interference detection technique based on computer generated hologram (CGH) was proposed. Firstly, the detection principle and method of this technology were described in detail, and the key technical points in the processing of testing CGH and alignment CGH design were given. Then, combined with engineering application, the corresponding CGH was designed and manufactured for convex aspheric with the aperture of 15 mm, the vertex curvature radius of 11.721 mm and its asphericity of 72 μm, and the null test interference detection experiments based on CGH were completed. Finally, the accuracy of the proposed method was verified by cross-comparison with Luphoscan detection technique. This technology provides an effective method for high-precision testing of small aperture convex aspheric and has significant engineering application value.
-
Key words:
- shape measurement /
- convex aspheric /
- computer generated hologram (CGH) /
- interference
-
图 1 CGH法检测凸非球面原理图
Figure 1. Schematic diagram of testing convex aspheric with CGH method
图 2 凸非球面参数与仿真结果。(a) 凸非球面参数；(b) 矢高与非球面度仿真结果
Figure 2. Convex aspheric parameters and simulation results. (a) Convex aspheric parameters; (b) Simulation results of vector height and asphericity
图 3 CGH检测凸非球面面形光路结构参数
Figure 3. Optical path structure parameters of convex aspheric detected by CGH
图 4 补偿测试全息设计结果。(a) 剩余波前差；(b) CGH相位与条纹频率分布
Figure 4. Test CGH design results. (a) Residual wavefront; (b) CGH phase and fringe frequency distribution
图 5 对准标记全息设计结果。(a) 剩余波前差；(b) CGH相位与条纹频率分布
Figure 5. Alignment CGH design results. (a) Residual wavefront; (b) CGH phase and fringe frequency distribution
图 7 CGH法测量凸非球面。(a) 检测现场；(b) 面形检测结果
Figure 7. Measurement of convex aspheric by CGH method. (a) Test site; (b) Test result of surface shape
图 8 Luphoscan法测量凸非球面。(a) 检测现场；(b) 面形检测结果
Figure 8. Measurement of convex aspheric by Luphoscan method. (a) Test site; (b) Surface shape test results
表 1 CGH设计结果与制造参数
Table 1. CGH design result and its manufacturing parameter
Parameters Test CGH Alignment CGH Manufacturing error CGH substrate material Corning 7980 - CGH substrate size 101.6 mm×101.6 mm×4.970 mm Thickness error: 0.002 mm
Transmission wavefront (RMS): 4.98 nmDiffraction type Phase Amplitude - Diffraction order +1 +3 - Width ratio 0.5 - Step height 460 nm - Step uniformity: 1.3% Aperture range 0-42 mm 43-50 mm - Fringe number 5260 1282 - Minimum fringe width About 2.4 μm About 3.0 μm - 
下载: 导出CSV
-
[1] Wang Shanshan, Hou Yinlong, Li Dawei, et al. 3D shape measurement of convex aspheric surface using reverse Hartmann test [J]. Optics Communications, 2020, 464(C): 125552. [2] Su Peng, Parks R E, Wang Lirong, et al. Software configurable optical test system: A computerized reverse Hartmann test [J]. Applied Optics, 2010, 49(23): 4404-4412. doi: 10.1364/AO.49.004404 [3] Yan Lilong, Zhu Deyan, Li Ming, et al. Research on compensating stitching testing for convex aspherical surface [J]. Optics Communications, 2020, 474: 126162. doi: 10.1016/j.optcom.2020.126162 [4] Yan Gongjing, Zhang Xianzhong. Research on non-null convex aspherical sub-aperture stitching detection technology [J]. Chinese Optics, 2018, 11(5): 798-803. (in Chinese) doi: 10.3788/co.20181105.0798 [5] Cai Zhihua, Wang Xiaokun, Hu Haixiang, et al. Non-null stitching test convex aspheric metal mirror [J]. Infrared and Laser Engineering, 2021, 50(11): 20210506. (in Chinese) doi: 10.3788/IRLA20210506 [6] Zhao Pengwei, Zhang Jinping, Ye Lu, et al. Catadioptric testing of large aperture convex hyperboloid surfaces [J]. Acta Optica Sinica, 2019, 39(11): 1122003. (in Chinese) [7] Ma Jie, Zhu Zheng. Testing convex aspherical surfaces with optimized modified Hindle arrangement [J]. Infrared and Laser Engineering, 2011, 40(2): 277-281. (in Chinese) doi: 10.3969/j.issn.1007-2276.2011.02.021 [8] Qi Lili, Zheng Liehua, Ye Lu, et al. Convex aspheric surface testing method using an autocollimation lens [J]. Acta Optica Sinica, 2020, 40(8): 0822001. (in Chinese) [9] Yao Jingang, Zheng Liehua Hao Peiming. Hindle testing of convex aspheric double-lens with zero-focal power [J]. Chinese Journal of Quantum Electronics, 2017, 34(3): 272-277. (in Chinese) [10] Wang Fengpu, Li Xinnan, Xu Chen, et al. Optical testing path design for LOT aspheric segmented mirrors with reflective-diffractive compensation [J]. Chinese Optics, 2021, 14(5): 1184-1193. (in Chinese) doi: 10.37188/CO.2020-0218 [11] Xia Zhigao, Chen Qiang. Study on an off-axis convex aspheric compensator [J]. Optics & Optoelectronic Technology, 2021, 19(4): 73-79. (in Chinese) [12] Xing Zhenchong, Zhang Bao, Hong Yongfeng. Design of compensator of convex aspheric surface with small apertures [J]. Chinese Journal of Lasers, 2015, 42(11): 1116001. (in Chinese) [13] Zhu Deyan, Wang Fang, Li Ping, et al. Research on hybrid compensation testing of convex aspherical mirror [J]. Optics and Lasers in Engineering, 2020, 132(C): 106108. [14] Dou Jiantai, Gao Zhishan, Yang Zhongming, et al. Deep aspheric surface test based on combination of computer generated holograms with low spatial frequency [J]. Acta Optica Sinica, 2016, 36(11): 1112004. (in Chinese) [15] He Li, Wu Zhonghua, Kang Yan, et al. High order aspheric testing with large asphericity, fast focal ratio and large diameter [J]. Laser & Optoelectronics Progress, 2016, 53(12): 122201. (in Chinese) [16] Li Shijie, Liu Bingcai, Tian Ailing, et al. A practical method for determining the accuracy of computer-generated holograms for off-axis aspheric surfaces [J]. Optics and Lasers in Engineering, 2016, 77: 154-161. [17] Qiu Hongwei, Jin Chunshui, Yu Jie, et al. CGH encoding with variable step size search [J]. Chinese Optics, 2021, 14(2): 368-374. (in Chinese) doi: 10.37188/CO.2020-0124 [18] 李世杰. 离轴非球面的组合全息检验[D]. 北京: 中国科学院大学, 2014. Li Shijie. Testing off-axis aspheric surface by combined-hologram[D]. Beijing: University of Chinese Academy of Sciences, 2014. (in Chinese) -
点击查看大图
计量
- 文章访问数: 109
- HTML全文浏览量: 12
- PDF下载量: 60
- 被引次数: 0
