下载:
-
近年来，飞秒激光制造技术作为一种高精密加工手段，凭借其真三维、加工方式灵活以及适用于多种材料等优势，被广泛应用于多种基础研究[1-5]。其中飞秒激光直写(FsDW)作为制备光子芯片的重要手段[6-8]，已经在国防建设、保密通讯和人工智能等领域发挥了重要作用。光波导作为光子芯片的基础单元，对其性质的完整表征对于设计高质量光子网络十分重要[9]。有效折射率是决定波导光学性质的关键性质[10]，其决定了波导的传播常数和相位信息[11-12]，在设计光子器件和相位匹配等方面具有重要意义。
目前，对于光波导有效折射率的测量工作研究很多，其中掩埋型的光波导的测量方式有以下两种。一种是通过测量波导的折射率分布，近似计算获得波导的有效折射率，该方法利用差分近场扫描显微镜光学显微镜(DNSOM)测量微分光场并结合亥姆霍兹方程逆算法，计算得到光波导的二维折射率分布和波导有效折射率[13-14]。另一种是利用干涉法通过对特定器件或波导原位测量获得波导的有效折射率。其中数值孔径法需要空间光和在波导传播后的光发生干涉，利用干涉条纹特性来反推波导的数值孔径(NA)，NA测量误差为30%，因此利用NA估算波导的有效折射率精度较低[15]。另外，从环形谐振器和马赫-曾德尔干涉仪（MZI）[16-17]等干涉结构中，也可以利用器件特性测量得到波导的有效折射率。目前该干涉方法主要应用在硅基波导结构[16]，实现了利用MZI测量硅波导与更宽尺寸波导的有效折射率差。飞秒激光直写玻璃波导有效折射率的测量工作中[17]，仅测量激光脉冲对原波导修饰后的有效折射率改变量，而不能精确测量波导的有效折射率绝对数值。
文中设计了一种两干涉臂断开的MZI结构，实现了原位测量玻璃波导的有效折射率。通过利用MZI结构两个干涉臂的断开长度差，使得两臂的光程差不断改变。不同光程差的干涉结果不同，实验上对其结果进行测量并计算出波导的有效折射率。研究了包含断线结构MZI的传输矩阵。结合对断线波导损耗的研究，对这种特殊MZI的结构进行了理论分析，在理论上证明了利用该结构可对波导的有效折射率进行原位测量。选取了不同断线长度MZI的输出结果，并与理论模拟结果进行对比。理论与实验结果吻合良好，进一步验证了该方法的可行性。
-
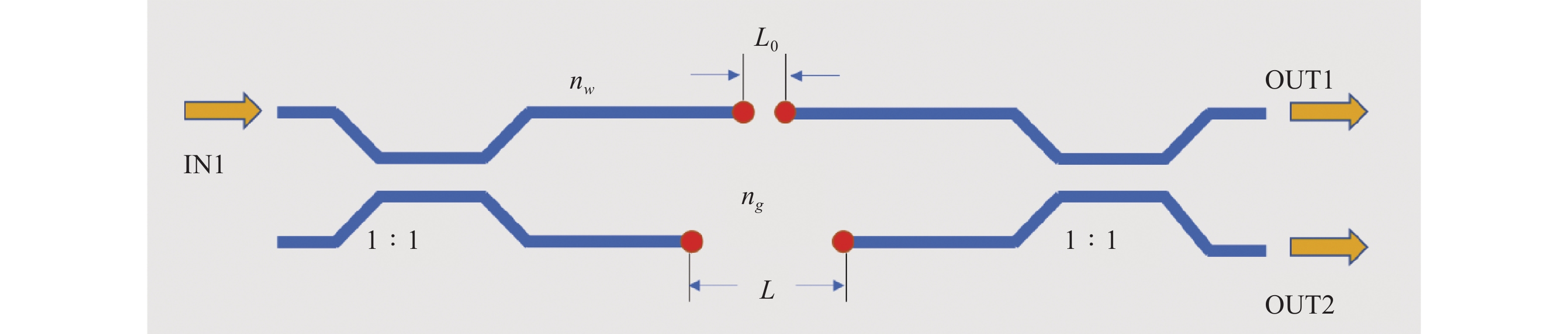
利用MZ干涉法测量了玻璃波导的有效折射率，设计结构如图1所示。MZI两干涉臂的断开长度不同产生光程差，最终在输出端口测量干涉结果。飞秒激光直写波导，在波导断开处会产生过度曝光点，带来额外的附加相位。制造干涉臂的光程差只需要断开其中一条干涉臂，MZI结构设计了两干涉臂光程相减消除过度曝光引起的额外相位。为L0=20 μm，另一条干涉臂的断开长度为L。激光从IN1口输入后，通过分光比为1∶1的定向耦合器（DC）将光束均分到两干涉臂，由于两干涉臂的断开长度不同，两束激光在干涉臂传输后产生光程差，在干涉仪后端的DC耦合区域干涉后输出。光束在MZI传输过程中，两个干涉臂相位公式如下：
$$ {\phi }_{1}={k}_{0}{n}_{w}\left({L}_{t}-{L}_{0}\right)+{k}_{0}{n}_{g}{L}_{0}+{\phi }_{1}{'} $$ (1) $$ {\phi }_{2}={k}_{0}{n}_{w}\left({L}_{t}-L\right)+{k}_{0}{n}_{g}L+{\phi }_{2}{'} $$ (2) 式中：
${\phi }_{1} $ 和${\phi }_{2} $ 分别为光束通过两个干涉臂的相位改变量；k0nw(Lt−L0)和k0nw(Lt−L)为光束在波导区域的相位改变量；k0ngL0和k0ngL为光束在断开区域的相位改变量；${\phi }'_{1} $ 和${\phi }'_{2} $ 为分别为两臂断开处引起的附加相位。其中，Lt为两个干涉臂的总长度，nw为波导的有效折射率，ng为玻璃基底的折射率，k0为真空波数。可得相位差公式如下：$$ \Delta \phi ={k}_{0}\cdot \Delta n\cdot \left(L-{L}_{0}\right)+\Delta \phi {'} $$ (3) 式中：∆n为玻璃折射率与波导有效折射率的差值；
$\Delta \phi {'} $ 是由于波导中断后，高斯光束在自由空间传播时引起的附加几何相位。
图 1 断臂MZI结构示意图，由两个分光比为1∶1的定向耦合器和断线波导组成。IN1为激光输入端口，OUT1和OUT2为两个输出端口
Figure 1. Schematic diagram of the structure of the breaking arm MZI, consisting of two directional couplers with a splitting ratio of 1∶1 and a breaking line waveguide. IN1 is the laser input port, OUT1 and OUT2 are the two output ports
测量波导有效折射率的关键在于将断线MZI的输出结果与相位差联系起来，对其关系式进行研究。实验中采用单模光束传输条件，研究了单模传输条件下的MZI透射比公式。首先需要对MZI的传输矩阵进行求解，传输矩阵如下：
$$ \begin{split} \left[\begin{array}{c}E3\\ E4\end{array}\right]=& \left[\begin{array}{cc}\sqrt{1-C}& -i\sqrt C\\ -i\sqrt C& \sqrt{1-C}\end{array}\right]\left[\begin{array}{cc}{{\rm{e}}}^{-i{\phi }_{1}-{\alpha }_{1}}& 0\\ 0& {{\rm{e}}}^{-i{\phi }_{2}-{\alpha }_{2}}\end{array}\right]\cdot\\ &\left[\begin{array}{cc}\sqrt{1-C}& -i\sqrt C\\ -i\sqrt C & \sqrt{1-C}\end{array}\right]\left[\begin{array}{c}E1\\ 0\end{array}\right] \end{split} $$ (4) 式中：E3和E4分别为OUT1和OUT2的电场强度；等式右边第一个矩阵和第三个矩阵为光束在DC的传输矩阵；C为图1中两个定向耦合器的分束比；等式右边第二个矩阵为光束在两个断臂中的传输矩阵，其中
${\phi }_{1} $ 和α1分别为光束通过MZI干涉臂上臂的相位和损耗，对应的${\phi }_{2} $ 和α2为分别为光束通过MZI干涉臂下臂的相位和损耗；E1为输入光的电场强度。对传输矩阵（4）进行求解，令C=0.5，可以得到两输出端电场强度的表达式：$$ E3 = \frac{E1}{2}\left({{\rm{e}}}^{-i{\phi }_{1}-{\alpha }_{1}}-{{\rm{e}}}^{-i{\phi }_{2}-{\alpha }_{2}}\right) $$ (5) $$ E4 = \frac{-i\cdot E1}{2}\left({{\rm{e}}}^{-i{\phi }_{1}-{\alpha }_{1}}+{{\rm{e}}}^{-i{\phi }_{2}-{\alpha }_{2}}\right) $$ (6) $$ {{\rm{e}}}^{ix}=\mathrm{cos}x+i\cdot \mathrm{sin}x $$ (7) $$ P={\left|E\right|}^{2} $$ (8) 利用欧拉公式（7）对公式（2）和公式（3）进行化简，再代入公式（8），求解得到OUT1的输出光功率P3和OUT2的输出光功率P4公式如下：
$$ P3=\frac{P1}{4}\left[{{\rm{e}}}^{-{2\alpha }_{1}}+{{\rm{e}}}^{-{2\alpha }_{2}}-2{{\rm{e}}}^{-{\alpha }_{1}-{\alpha }_{2}}\mathrm{cos}\left({\phi }_{1}-{\phi }_{2}\right)\right] $$ (9) $$ P4=\frac{P1}{4}\left[{{\rm{e}}}^{-{2\alpha }_{1}}+{{\rm{e}}}^{-{2\alpha }_{2}}+2{{\rm{e}}}^{-{\alpha }_{1}-{\alpha }_{2}}\mathrm{cos}\left({\phi }_{1}-{\phi }_{2}\right)\right] $$ (10) 由公式（9）和公式（10）可以计算得到透射比的公式如下：
$$ T=\frac{P4}{P3+P4}=\frac{1}{2}+\frac{{{\rm{e}}}^{-{\alpha }_{1}-{\alpha }_{2}}\mathit{{\rm{cos}}}\left({\phi }_{1}-{\phi }_{2}\right)}{{{\rm{e}}}^{-{2\alpha }_{1}}+{{\rm{e}}}^{-{2\alpha }_{2}}} $$ (11) 公式（11）中，损耗因子公式如下：
$$ {\alpha }_{1}={\alpha }_{d1}+{\alpha }_{0} $$ (12) $$ {\alpha }_{2}={\alpha }_{d2}+{\alpha }_{L} $$ (13) 因此，损耗主要考虑两部分因素，其中αd1
和αd2为直波导区域引起的损耗，α0和αL为两臂断开引起的损耗。分析透射比公式可以发现，当L值改变时，会引起两个干涉臂相位差发生变化，同时导致断开长度为L的干涉臂损耗发生改变，即损耗与断线长度L存在函数关系。该公式中有两个变量，为L和α2，以及未知量 $\Delta \phi {'} $ 。出于数据处理的需求，需要得到单一变量L和透射比T的具体关系表达式。因此，文中主要解决以下两个问题：首先，建立损耗α2和断开长度L的关系表达式，解决单一变量的问题；其次，建立附加相位$\Delta \phi {'} $ 的具体表达式，研究其与断开长度L的关系。
图 2 （a） 高斯光束在断线波导中的传播模型；（b）高斯光束在不同断线波导中传输光场的分布
Figure 2. (a) Model of Gaussian beam propagation in a disconnected waveguide; (b) Light field distribution of Gaussian beam propagation in waveguides with different breaking
为了研究损耗和波导断开长度的函数关系，采用了高斯光束在两个单模光纤中径向对接的传播模型，类比单模高斯光束在断开波导中的传播。图2（a）展示了断线波导中高斯光束的传播模型。
高斯光束从波导前端输入后，在玻璃介质中以高斯函数的形式传播。它的振幅沿着传播方向z从中心向外平滑地减少。因此，随着传播距离L的增加，输出波导端口收集到的光强越弱。其中，z=0时，2w0为波导的模场直径，2w(L)为断开长度为L时的束腰直径。高斯光束在传播过程中，其电磁场满足亥姆霍兹方程，在缓变振幅近似条件下，可得到高斯光束在z=0处开始，将以如公式（14）中的非均匀高斯球面波的形式在自由空间传播。
$$ {E}\left({r},{z}\right) = \frac{{A}_{0}{w}_{0}}{\left.w(z\right)}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{{r}^{2}}{{w}^{2}\left(z\right)}\right]{\rm{exp}}\left\{-i\left\{k\left[\frac{{r}^{2}}{2R\left(z\right)}+z\right] - \psi \left(z\right)\right\}\right\} $$ (14) 式中：r为高斯光束的半径；z为传播距离；A0为高斯光束的振幅常量；波数k = 2π/λ，λ为波长；w(z)为传播距离为z时，高斯光束的束腰半径；w0为z=0时，高斯光束的束腰半径；R(z)为高斯光束的等相面曲率半径；
$\psi \left(z\right) $ 为高斯光束的相位因子。其表达式如下：$$ \psi \left(z\right)={{\rm{arctan}}}\left(\frac{\lambda z}{\pi {{w}_{0}}^{2}}\right) $$ (15) 由公式（6）可知，光束在自由空间传播后产生的总相移为：
$$ \mathrm{\phi }({r},{z})=k\left[\frac{{r}^{2}}{2R\left(z\right)}+z\right]-\psi \left(z\right) $$ (16) 它表征的是高斯光束在点（r, z）处相对于原点（0, 0）产生的相位差。式中：kz为几何位移；
$ k\dfrac{{r}^{2}}{2 R\left(z\right)} $ 表示与径向相关的位移；$\psi \left(z\right) $ 为高斯光束在空间传播距离z时，相对几何位移产生的附加相位。高斯光束在MZI中传播时，只考虑几何位移产生的相位改变量，因此可以忽略掉与径向相关的位移。将公式（16）应用到MZI断开的干涉臂中，可得到附加相位
$\Delta \phi {'} $ 和断开长度L的对应关系：$$ \Delta {\phi }^{{'}}={{{{\rm{arctan}}}}}\left(\frac{\lambda L}{\pi {{w}_{0}}^{2}}\right) $$ (17) 高斯光斑在波导断开处出射后，随着断开长度L增大，光斑模场直径逐渐增大，光功率密度逐渐降低，在有限的波导的模场直径下接收到的光功率越少。根据高斯光束在自由空间的传播原理，束腰半径与传播距离L的公式如下：
$$ W={w}_{0}\sqrt{1+{\left(\frac{\lambda L}{\pi {n}_{g}{{w}_{0}}^{2}}\right)}^{2}} $$ (18) 式中：λ为传输光束的波长。在图3（a）中模拟了高斯光束的束腰半径在两种介质中传播时对应的变化曲线。图中蓝色曲线是折射率n1
=1，红色曲线是折射率n2=1.504，为玻璃折射率。在图3（b）中模拟了高斯光斑从波导出射后在玻璃介质中的发散情况，分别展示了传播距离为50 μm，400 μm，500 μm和1000 μm的模式分布图。光束的发散结果与图3（a）的计算结果相符合。利用高斯光束在径向对接光纤的原理，引起的插入损耗公式如下： $$ \frac{P 1}{P}=\frac{1}{1+\left(\dfrac{L}{k_g w_0^2}\right)^2} $$ (19) 式中：kg为光纤端面间隙的波数。将上述公式应用到波导结构中，w0即为单模波导的模场半径。
图 3 (a) w0=4 μm时，不同背景折射率下束腰半径与传播距离L的关系；(b)模拟高斯光斑在折射率为n2的材料内部发散的模场分布图
Figure 3. (a) Beam waist radius versus propagation distance L for different background refractive indices at w0=4 μm; (b) Simulated mode field distribution of Gaussian light diverging inside a material with refractive index n2
-
文中使用飞秒激光直写技术制备波导结构，在实验上探索了以上模型的可行性。实验中采用的飞秒激光器（Light Conversion, Carbide 5 W）脉冲宽度和中心波长分别为290 fs和1030 nm，加工深度和扫描速度分别为170 μm和40 mm/s。所用材料为硼硅酸盐玻璃(康宁，Eagle2000)。在该实验条件下制备了如图2（b）所示的直波导与断线波导。使用808 nm的连续激光对波导测试其损耗结果，分别测量了相同长度的直波导和断线波导的输出功率P和P1。利用公式(19)对测量结果进行处理，拟合得到了图4(b)中的红色曲线，拟合置信度高达97.23%。其中图4（a）为理论模拟的断线损耗数据曲线，对比之下，理论与实验高度吻合，证明了该模型的准确性。
图 4 （a）理论模拟断线波导损耗与断线长度L的关系；（b） 实验测量的断线波导损耗与断线长度L的关系，插图为波导端面的显微镜图
Figure 4. (a) Theoretical simulation of disconnected waveguide loss versus breaking length L; (b) Experimentally measured disconnected waveguide loss versus breaking length L, the inset is a microscope image of the waveguide end face
从图4（b）中可以看出，随着断开长度的增加拟合曲线逐渐偏移。该偏移由两个因素导致：一是波导模场不是标准的圆形波导；二是实验上波导损耗越大，杂散光越强，引起的测量误差越大。根据图4的实验结果，验证了高斯光束在断开波导的损耗模型是合理可行的。因此，在干涉臂断开引起的损耗可以得到完整的表达式，即：
$$ {{\rm{e}}}^{-\alpha }=\dfrac{1}{1+{\left(\dfrac{L}{{k}_{g}{{w}_{0}}^{2}}\right)}^{2}} $$ (20) 将公式（17）和（20）代入到MZI透射比公式（2）中，能够得到单一变量的透射比公式，利用该公式对实验数据进行处理即可得到波导的有效折射率差值。
图 5 断臂MZI器件的模拟光场
Figure 5. Simulated optical field of a breaking arm MZI device
在后续的工作中，理论模拟了激光在断臂MZI结构的传输模型，如图5所示。图中，固定右边的干涉臂断开长度为20 μm，分别展示了左边干涉臂断开长度不同的输出光强分布。输出光强随着干涉臂断开长度的增加，总输出光强由于断臂损耗的增加而减小，其透射比呈现一个阻尼震荡的变化。
为了证明该方法在飞秒激光制备波导上应用的可行性，制备了多个不同断开长度L的MZI结构，断开长度L分别为20 μm，200 μm，500 μm和1000 μm。其透射比测量结果如图6所示，与理论模拟结果进行对比，随着断开长度L的增加，透射比呈现相同的变化趋势。理论与实验的数值较为一致，验证了该方法在实验上的可行性。理论与实验MZI透射比存在轻微的差异，这种差异是由于模拟的波导参数与实验制备的波导不同。利用透射比公式对图6的实验数据和模拟数据进行处理，分别拟合获得波导的有效折射率。其中实验测量的有效折射率差Δn为7.7×10−4，模拟获得的有效折射率差
Δn为7.3×10−4。 
图 6 MZI透射比的实测与模拟柱状图
Figure 6. Measured and simulated histogram of MZI transmission
-
文中提出了一种断臂MZI结构，实现了对飞秒激光直写玻璃波导有效折射率的准确测量。通过分析MZI出射光束能量分布，得到波导有效折射率为1.504+7.7×10−4，其中玻璃折射率为1.504。此外，在理论上分析了该结构的工作原理，建立了断线波导的高斯光束传播模型，模拟和实验分别证明了该模型的可行性。该方法具有直接测量和高精度测量等优势，对于未来光量子芯片制备和设计具有重要意义。
In-situ measurement of effective refractive index of glass waveguides (invited)
-
摘要: 飞秒激光直写玻璃波导是快速制备三维集成光子芯片的一种重要手段，波导有效折射率的准确测量对于设计光子器件意义重大。设计并制备了一种断臂马赫-曾德尔干涉仪（MZI）结构对玻璃波导有效折射率进行原位精密测量。激光在断线区域和波导内的有效折射率不同，在传输相同长度下产生一定的相位差，最终导致不同的干涉结果。对断臂MZI结构的相位干涉结果进行处理，得到激光直写玻璃波导的有效折射率为1.504+7.7×10−4。利用RSOFT软件光束传播算法对器件进行模拟仿真，仿真结果与实验吻合良好。该精确测量玻璃波导有效折射率的方法对于提升光子芯片设计与制造能力具有重要意义。Abstract: Femtosecond laser direct writing of glass waveguides is an important means to rapidly prepare three-dimensional integrated photonic chips, and the accurate measurement of the effective refractive index of waveguides is significant for designing photonic devices. A breaking-arm Mach-Zendel interferometer (MZI) structure is designed and fabricated for in-situ precise measurement of the effective refractive index of glass waveguides. The different effective refractive index of the laser in the breaking region and within the waveguide produces a certain phase difference at the same length of transmission, which eventually leads to different interference results. The phase interference results of the MZI of the breaking arm are processed to obtain the effective refractive index of the laser direct-written glass waveguide as 1.504+7.7×10−4. The device is simulated by using the beam propagation algorithm of RSOFT, and the simulation results are in good agreement with the experimental results. This accurate measurement of the effective refractive index of the glass waveguide is of great significance for the enhancement of photonic chip design and fabrication.
-
图 1 断臂MZI结构示意图，由两个分光比为1∶1的定向耦合器和断线波导组成。IN1为激光输入端口，OUT1和OUT2为两个输出端口
Figure 1. Schematic diagram of the structure of the breaking arm MZI, consisting of two directional couplers with a splitting ratio of 1∶1 and a breaking line waveguide. IN1 is the laser input port, OUT1 and OUT2 are the two output ports
图 2 （a） 高斯光束在断线波导中的传播模型；（b）高斯光束在不同断线波导中传输光场的分布
Figure 2. (a) Model of Gaussian beam propagation in a disconnected waveguide; (b) Light field distribution of Gaussian beam propagation in waveguides with different breaking
图 3 (a) w0=4 μm时，不同背景折射率下束腰半径与传播距离L的关系；(b)模拟高斯光斑在折射率为n2的材料内部发散的模场分布图
Figure 3. (a) Beam waist radius versus propagation distance L for different background refractive indices at w0=4 μm; (b) Simulated mode field distribution of Gaussian light diverging inside a material with refractive index n2
图 4 （a）理论模拟断线波导损耗与断线长度L的关系；（b） 实验测量的断线波导损耗与断线长度L的关系，插图为波导端面的显微镜图
Figure 4. (a) Theoretical simulation of disconnected waveguide loss versus breaking length L; (b) Experimentally measured disconnected waveguide loss versus breaking length L, the inset is a microscope image of the waveguide end face
-
[1] Sun Shufeng, Wang Pingping. Micro/nano structures fabricated by two-photon photopolymerization of femtosecond laser [J]. Infrared and Laser Engineering, 2018, 47(12): 1206009. (in Chinese) doi: 10.3788/IRLA201847.1206009 [2] Gross S, Riesen N, Love J D, et al. Three-dimensional ultra-broadband integrated tapered mode multiplexers [J]. Laser & Photonics Reviews, 2014, 8(5): L81-L85. doi: 10.1002/lpor.201400078 [3] Gross S, Withford M J. Ultrafast-laser-inscribed 3D integrated photonics: challenges and emerging applications [J]. Nanophotonics, 2015, 4(3): 332-352. doi: 10.1515/nanoph-2015-0020 [4] Li Zhiming, Wang Xi, Nie Jinsong, et al. High frequency femtosecond laser induced periodic spatial structure on silicon surface [J]. Infrared and Laser Engineering, 2018, 47(1): 0106003. (in Chinese) doi: 10.3788/IRLA201847.0106003 [5] Zhang Bin, Li Ziqi, Wang Lei, et al. Research advances in laser crystal optical waveguides fabricated by femtosecond laser direct writing [J]. Laser & Optoelectronics Progress, 2020, 57(11): 111415. doi: 10.3788/LOP57.111415 [6] Yu F, Zhang X L, Tian Z N, et al. General rules governing the dynamical encircling of an arbitrary number of exceptional points [J]. Physical Review Letters, 2021, 127(25): 253901. doi: 10.1103/PhysRevLett.127.253901 [7] Ocier C R, Richards C A, Bacon-Brown D A, et al. Direct laser writing of volumetric gradient index lenses and waveguides [J]. Light: Science & Applications, 2020, 9(1): 196. doi: 10.1038/s41377-020-00431-3 [8] Cerjan A, Wang M, Huang S. Thouless pumping in disordered photonic systems [J]. Light: Science & Applications, 2020, 9(1): 178. doi: 10.1038/s41377-020-00408-2 [9] Goi E, Zhang Q, Chen X, et al. Perspective on photonic memristive neuromorphic computing [J]. PhotoniX, 2020, 1(1): 3. doi: 10.1186/s43074-020-0001-6 [10] Zhang Y, Wu J, Wang L, et al. Femtosecond laser direct writing of Nd: YAG waveguide with Type I modification: Positive refractive index change in track [J]. Optical Materials, 2021, 113: 110844. doi: 10.1016/j.optmat.2021.110844 [11] Shams El-Din M A, Koerdt M, Wochnowski C, et al. Investigation of a UV-laser generated waveguide in a planar polymer chip using an improved interferometric method [J]. Optics and Lasers in Engineering, 2012, 50(3): 405-412. doi: 10.1016/j.optlaseng.2011.10.015 [12] Park J, Lee B. An Approximate formula of the effective refractive index of the metal-insulator-metal surface plasmon polariton waveguide in the infrared region [J]. Japanese Journal of Applied Physics, 2008, 47(11): 8449-8451. doi: 10.1143/JJAP.47.8449 [13] Tsai W S, Ting S Y, Wei P K. Refractive index profiling of an optical waveguide from the determination of the effective index with measured differential fields [J]. Opt Express, 2012, 20(24): 26766-26777. doi: 10.1364/OE.20.026766 [14] Popescu V A. Determination of propagation constants in a Ti: LiNbO3 optical waveguide by using finite element and variational methods [J]. Optics Communications, 2005, 250(4): 274-279. [15] Homoelle D, Wielandy S, Gaeta A L, et al. Infrared photosensitivity in silica glasses exposed to femtosecond laser pulses [J]. Optics Letters, 1999, 24(18): 1311-1313. doi: 10.1364/OL.24.001311 [16] Dattner Y, Yadid-Pecht O. Analysis of the effective refractive index of silicon waveguides through the constructive and destructive interference in a Mach-Zehnder interferometer [J]. IEEE Photonics Journal, 2011, 3(6): 1123-1132. doi: 10.1109/JPHOT.2011.2171678 [17] Matthias W, Jonas B, Stefan N, et al. Measurement of fs laser-induced refractive index changes using an integrated optical interferometer [C]//SPIE, 2003, 4978: 214-221. -
点击查看大图
计量
- 文章访问数: 179
- HTML全文浏览量: 66
- PDF下载量: 60
- 被引次数: 0
