-
成像系统设计中提到的自由曲面一般指没有回转对称轴的曲面。相对于传统球面和非球面，自由曲面在数学描述上有更多的变量，可以用于设计得到像质与指标更高、元件数量更少、体积更小、质量更轻、结构更紧凑的成像系统[1-3]。自由曲面的提出与应用被认为是成像光学设计领域的革命性发展[4]，在遥感成像[5-8]、增强现实[9-10]、新型相机[11]、光谱分析[12-13]、光刻物镜[14]等方向都有突出的应用。
在设计自由曲面成像系统过程中，除了要尽可能地提升系统的成像质量并且满足一定的约束条件，还要考虑曲面的工艺性，即应该使曲面尽可能地容易被加工。而曲面的检测精度很大程度上决定了曲面的加工精度。零位干涉法是目前一种常见的高精度自由曲面面形检测方法，可以设计并加工计算全息元件（CGH）调控波前使其与待测自由曲面匹配。为了降低CGH的加工难度与曲面检测难度，自由曲面整体矢高相对于基底球面或者二次曲面的矢高的偏差应该尽量小。采用传统的复曲面、XY多项式自由曲面等，只能通过选取曲面上的离散的特征点，计算特征点处的曲面总矢高和基底曲面间的矢高差并进行控制。如果特征点的数量较多，则系统优化速度较慢，效率低。而采用带有正交性的多项式叠加在基底上来描述自由曲面则可以更简单地解决以上问题，因为正交多项式的系数平方和同曲面与基底曲面间的矢高偏差在数学上是相关的。对于回转对称系统，由于系统中各个曲面的通光孔径一般都是圆形，此时采用常用的Zernike多项式自由曲面以及Q2D多项式自由曲面即可以实现较好的矢高差控制。例如，N. Takaki等人提出了采用球面或者离轴二次曲面基底的Zernike多项式自由曲面以及Q2D多项式自由曲面的设计方法[15-16]，实现了在系统设计过程中实时表征与控制曲面的检测难度。但是一般的自由曲面成像系统，其视场多为矩形视场，因此即使系统的孔径光阑为圆形，系统中的其他曲面实际的通光区域基本上也是矩形。此时，如果仍采用在圆域正交的多项式，就需要在矩形孔径的外接圆或者内接圆使用其正交性，对于实际矩形孔径内的矢高差的控制作用有限。
基于以上问题，研究了方域内正交的Chebyshev多项式和Legendre多项式在自由曲面成像系统设计中的应用。根据两种面型的数学表达式以及其性质，推导出相关的数学约束方法，有效且高效地降低矩形孔径的自由曲面相对于其基底曲面的矢高差，进而降低曲面的检测难度与加工难度。通过多个设计实例验证了所提出方法的有效性。
-
$$ \left\{ \begin{gathered} \left\langle {{P_n},{P_{n'}}} \right\rangle = {0}\;{\rm{when}}\;n \ne n' \\ \left\langle {{P_n},{P_{n'}}} \right\rangle \ne {0_{}}\;{\rm{when}}\;n{\text{ = }}n' \\ \end{gathered} \right. $$ (1) 式中：运算符号<f, g>表示基函数f与g的内积（给定区域内的加权积分）。当满足正交条件时，用正交集描述定义域内的其他函数时，其对应的系数集是唯一的。当区域为方形孔径时，有：
$$ \left\langle {f,g} \right\rangle = \frac{{\displaystyle\int_{ - 1}^1 {\displaystyle\int_{ - 1}^1 {f(u,v)g(u,v)w(u,v){\text{d}}u{\text{d}}v} } }}{{\displaystyle\int_{ - 1}^1 {\displaystyle\int_{ - 1}^1 {w(u,v){\text{d}}u{\text{d}}v} } }} $$ (2) 式中：w(u, v)为权函数，在归一化孔径下，u和v取值范围均为[−1, 1]。用于光学设计的多项式曲面一般有一个球面或者二次曲面基底。多项式自由曲面同基底曲面的矢高差可以描述为多项式的线性组合，即为S=ΣαnPn。矢高差自身的内积运算结果和曲面同基底曲面间矢高差的平方和值相关。对于一般自由曲面，内积运算结果为：
$$ \left\langle {S,S} \right\rangle = \sum\limits_n {\left\langle {S,{\alpha _n}{P_n}} \right\rangle } = \sum\limits_n {\left\langle {{P_n},{P_n}} \right\rangle } \alpha _n^2 $$ (3) 公式（3）适用于所有正交性多项式。通过计算正交多项式系数平方和即可在一定程度上将加工制造评估与内积运算相联系。另外，在优化设计过程中将其添加为约束条件进行控制，可以实现自由曲面的可检测性实时估计，而基本不会减慢优化设计过程。文中探讨两种常见的方域正交多项式，分别为二维Chebyshev多项式和二维Legendre多项式。这两类多项式属于Jacobian正交多项式，其表达式中坐标x、y部分相互分离。
-
Chebyshev多项式可分为第一类Chebyshev多项式以及第二类Chebyshev多项式，文中讨论的是第一类。x方向上的一维Chebyshev多项式在区间[−1, 1]上关于权函数w(x)=1/(1−x2)0.5是正交的，如公式（4）所示，y方向上同理。
$$ \int_{{{ - 1}}}^{\text{1}} {\frac{{{T_n}(x){T_m}(x)}}{{\sqrt {1 - {x^2}} }}} {\text{d}}x = \left\{ \begin{gathered} \frac{1}{2}\pi {\delta _{nm}}\mathop {}\nolimits^{} \;{\rm{when}}\; \mathop {}\nolimits^{} n \ne 0,m \ne 0 \\ \pi \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \;{\rm{when}}\; \mathop {}\nolimits^{} n = m = 0 \\ \end{gathered} \right. $$ (4) 式中：δnm为克罗内克函数（Kronecker Delta），当n=m时，δnm=1；当n≠m时，δnm=0。x方向上非归一化Chebyshev多项式的前六阶如表1所示。
表 1 前六阶一维Chebyshev多项式
Table 1. 1D Chebyshev polynomial up to the sixth order
n Tn(u) 0 1 1 u 2 2u2−1 3 4u3−3u 4 8u4−8u2+1 5 16u5−20u3+5u 6 32u6−48u4+18u2−1 二维Chebyshev多项式由x和y两个方向上的一维Chebyshev多项式相乘得到，二维Chebyshev多项式曲面由基底曲面和二维Chebyshev多项式相加得到，表达式为：
$$ \begin{split} z(x,y) =& \frac{{c({x^2} + {y^2})}}{{1 + \sqrt {1 - (1 + k){c^2}({x^2} + {y^2})} }} + \\ & \sum\limits_{i = 0}^N {\sum\limits_{j = 0}^M {{\alpha _{i,j}} \cdot {T_i}(u)} } \cdot {T_j}(v) \\[-5pt] \end{split} $$ (5) 式中：c为基底曲面顶点处的曲率；k为二次曲面系数；Ti(u)和Ti(v)为一维Chebyshev多项式，u=x/x0，v=y/y0，x0、y0则为x、y方向上归一化孔径值，如此即将矩形域归一化到了一个单位方域（边长为2）；N和M为x和y方向上Chebyshev多项式的阶数；αi,j为相应的多项式系数。大多数系统设计时用到的面形关于YOZ平面对称，因此文中后续讨论系统设计中使用的多项式不含x的奇数阶，不妨在此令i=2t。
由于Chebyshev多项式的权函数并非常数，而是与自变量相关的函数，因此对Chebyshev多项式自由曲面的矢高差自身进行内积运算时，其结果不同于Q2D多项式那样是多项式的系数平方和，而是一个比较复杂的函数。因此，优化过程中对Chebyshev多项式自由曲面的面形矢高差进行控制时，直接对系数平方和进行约束并不完善，但仍可以通过控制矩形孔径边缘处的曲面同基底曲面间的矢高差之和平均值为零来降低整个矩形孔径内部的矢高差，降低曲面的检测难度。
图1所示为矩形孔径示意图。为了控制曲面同基底曲面之间的矢高差，可以通过控制孔径边缘（AB、BC、CD、DA四段）处曲面与基底曲面间矢高差之和为0进行约束。以AB段（对应v=1）为例，AB段的曲面同基底曲面间的矢高差之和为Chebyshev多项式在v=1时从u=−1~+1上的积分值，如公式（6）所示。在设计优化过程中使用到的多项式阶数不会太高，而且高阶项对系统像差的校正贡献不大，文中只考虑了不高于六阶的多项式。此时需满足2t+j≤6。
图 1 矩形曲面孔径示意图
Figure 1. Sketch of the rectangular surface aperture
$$ \begin{split} zsa{g_{{\text{sum}}}}(AB) =& \int_{ - 1}^1 {\sum\limits_{t = 0}^{\text{3}} {\sum\limits_{j = 0}^{6 - 2t} {{a_{2t,j}} \cdot {T_{{\text{2}}t}}(u){\text{d}}u} } } {{ = }}\\ & 2\sum\limits_{j = 0}^6 {{\alpha _{0,j}}} - \frac{2}{3}\sum\limits_{j = 0}^4 {{\alpha _{2,j}}} - \frac{2}{{15}}\sum\limits_{j = 0}^2 {{\alpha _{4,j}}} - \frac{2}{{35}}{\alpha _{6,0}} \\ \end{split} $$ (6) 计算可得其余边缘处曲面同基底曲面间矢高差之和与系数关系如公式（7）所示：
$$ \begin{split} zsa{g_{{\text{sum}}}}(CD) =& 2\sum\limits_{j = 0}^6 {{{( - 1)}^j}{\alpha _{0,j}}} - \frac{2}{3}\sum\limits_{j = 0}^4 {{{( - 1)}^j}{\alpha _{2,j}}} -\\ & \frac{2}{{15}}\sum\limits_{j = 0}^2 {{{( - 1)}^j}{\alpha _{4,j}}} - \frac{2}{{35}}{\alpha _{6,0}} \\ zsa{g_{{\text{sum}}}}(BC) =& 2\sum\limits_{t = 0}^3 {{\alpha _{2t,0}}} - \frac{2}{3}\sum\limits_{t = 0}^2 {{\alpha _{2t,2}}} -\\ & \frac{2}{{15}}\sum\limits_{t = 0}^1 {{\alpha _{2t,4}}} - \frac{2}{{35}}{\alpha _{0,6}} \\ zsa{g_{{\text{sum}}}}(DA) =& 2\sum\limits_{t = 0}^3 {{\alpha _{2t,0}}} - \frac{2}{3}\sum\limits_{t = 0}^2 {{\alpha _{2t,2}}} -\\ & \frac{2}{{15}}\sum\limits_{t = 0}^1 {{\alpha _{2t,4}}} - \frac{2}{{35}}{\alpha _{0,6}} \\[-5pt] \end{split} $$ (7) 将四段边缘处的矢高差相加，得到孔径边缘上曲面同基底曲面间矢高差之和zsagsum，如公式（8）所示：
$$ \begin{split} zsa{g_{{\text{sum}}}} =& zsa{g_{{\text{sum}}}}(AB) + zsa{g_{{\text{sum}}}}(BC) + zsa{g_{{\text{sum}}}}(CD) + \\ & zsa{g_{{\text{sum}}}}(DA) = {\text{8}}{\alpha _{{\text{0,0}}}}{\text{ + }}\frac{8}{3}({\alpha _{{\text{0,2}}}} + {\alpha _{{\text{2,0}}}} - {\alpha _{{\text{2,2}}}}) + \\ & \frac{{56}}{{15}}({\alpha _{{\text{0,4}}}} + {\alpha _{{\text{4,0}}}}) + \frac{{136}}{{15}}({\alpha _{0,6}} + {\alpha _{6,0}}) - \frac{8}{5}({\alpha _{2,4}} + {\alpha _{4,2}}) \\ \end{split} $$ (8) 不难发现，zsagsum与部分系数的线性运算结果相关，在设计优化中可将其等于0添加为约束条件，实现曲面检测难度控制。考虑到多项式中的piston项以及y的一次幂项（tilt）需控制为零，需要添加系数约束条件，将某些系数的线性组合约束为0，消除由多项式自身带来的piston项以及tilt项。
$$ \begin{split} {\text{piston}} =& {\alpha _{{\text{0,0}}}} - {\alpha _{{\text{2,0}}}} - {\alpha _{{\text{0,2}}}} + {\alpha _{{\text{4,0}}}} + {\alpha _{{\text{2,2}}}} + {\alpha _{{\text{0,4}}}} - {\alpha _{{\text{6,0}}}} - {\alpha _{{\text{4,2}}}} -\\ & {\alpha _{{\text{2,4}}}} - {\alpha _{{\text{0,6}}}} = 0 \\ {\text{tilt}} =& {\alpha _{{\text{0,1}}}} - {\text{3}}{\alpha _{{\text{0,3}}}}{\text{ + 5}}{\alpha _{{\text{0,5}}}} -{\alpha _{{\text{2,1}}}} + 3{\alpha _{{\text{2,3}}}} + {\alpha _{{\text{4,1}}}} = 0 \\[-10pt] \end{split} $$ (9) 利用系数平方和约束曲面的矢高差特性虽然不太适用于Chebyshev多项式自由曲面设计，但在Legendre正交多项式自由曲面中却适用。
-
二维Legendre多项式是通过x、y方向上的一维Legendre多项式相乘获得。和Chebyshev多项式一样，其正交性也是在归一化孔径下成立。在边长分别为x0、y0的矩形孔径内，x、y方向上的归一化坐标变量为u和v，其中u=x/x0，v=y/y0，u、v的定义域均为[−1, 1]。如此即将矩形域归一化到了一个单位方域（边长为2）。x方向的一维Legendre多项式Pn(u)在区间[−1, 1]上相对权函数w(u)=1正交，有：
$$ \int_{ - {\text{1}}}^{\text{1}} {{P_n}(u){P_m}(u){\text{d}}u = \frac{2}{{2n + 1}}} {\delta _{nm}} $$ (10) 归一化一维Legendre多项式Pn(u)的前六阶如表2所示。
表 2 前六阶一维Legendre多项式
Table 2. 1D Legendre polynomial up to the sixth order
n Pn(u) 0 1 1 $\sqrt {\text{3}} u$ 2 $(\sqrt {\text{5}} {\text{/2)(3}}{u^2} - 1)$ 3 $(\sqrt {\text{7}} {\text{/2)(5}}{u^{\text{3}}} - {\text{3}}u)$ 4 $({\text{3/8)(35}}{u^{\text{4}}} - {\text{30}}{u^2} + 3)$ 5 $(\sqrt {11} {\text{/8)(63}}{u^{\text{5}}} - {\text{70}}{u^3} + 15 u)$ 6 $(\sqrt {1{\text{3}}} {\text{/16)(231}}{u^{\text{6}}} - {\text{315}}{u^{\text{4}}} + 1{\text{0}}5{u^{\text{2}}} - 5)$ 对于归一化后的Legendre正交多项式，其正交特性有：
$$ \int_{ - {\text{1}}}^{\text{1}} {{P_n}(u){P_m}(u){\text{d}}u = {\text{2}}} {\delta _{nm}} $$ (11) y方向上的一维Legendre多项式，其表达式和x方向一致，只需将u替换为v即可，两个方向上的Legendre多项式具有相同正交特性。
在方形域内，二维Legendre多项式Li(u, v)通过两个方向上一维Legendre多项式相乘得到，为：
$$ {L_i}(u,v) = {P_n}(u){P_m}(v) $$ (12) 式中：i为二维Legendre多项式排序序号。对于二维Legendre多项式，正交特性为：
$$ \begin{split} & \int_{ - {{1}}}^{{1}} {\int_{ - {{1}}}^{{1}} {{L_i}(u,v){L_{i'}}} } (u,v){\text{d}}u{\text{d}}v =\\ & \int_{ - 1}^1 {P_k^2(u){\text{d}}u\int_{ - 1}^1 {P_{_{i - k}}^2(v){\text{d}}v} } = {\text{4}}{\delta _{i{i'}}} \\[-5pt] \end{split} $$ (13) 和Chebyshev多项式自由曲面类似，Legendre正交多项式自由曲面面形矢高表达式为：
$$ \begin{split} z =& \frac{{c({x^2} + {y^2})}}{{1 + \sqrt {1 - (1 + k){c^2}({x^2} + {y^2})} }} + \\ & \sum\limits_{n = 0}^N {\sum\limits_{m = 0}^M {{\alpha _{n,m}} \cdot {P_n}(u)} } \cdot {P_m}(v) \end{split} $$ (14) 根据第1.1节介绍，令曲面同基底面间的矢高偏差S=L(u, v)，对矢高偏差进行内积运算，结合公式（3）可得曲面同基底曲面间的矢高差平方和与多项式的系数平方和相对应，即：
$$ \begin{split} \left\langle {{{\left| {L(u,v)} \right|}^2}} \right\rangle =& \left\langle {\left( {\sum\limits_{n = 0}^N {\sum\limits_{m = 0}^M {{\alpha _{n,m}}{P_n}(u){P_m}(v)} } } \right)} \right\rangle\\ & \left\langle {\left( {\sum\limits_{n'= 0}^{N'} {\sum\limits_{m'= 0}^{M'} {{\alpha _{n',m'}}{P_{n'}}(u){P_{m'}}(v)} } } \right)} \right\rangle = {\text{4}}\sum\limits_{n = 0}^N {\sum\limits_{m = 0}^M {\alpha _{n,m}^{\text{2}}} } \end{split}$$ (15) 接下来，在优化设计过程中，可以将公式（15）引入误差函数中，得到系统优化的总误差函数，如公式(16)所示：
$$ {\varPhi _{{\text{total}}}} = {w_1}{\varPhi _{{\text{performance}}}} + {w_2}\sum\limits_{n = 0}^N {\sum\limits_{m = 0}^M {\alpha _{n,m}^{\text{2}}} } $$ (16) 式中：Φperformance为系统成像质量（和某些约束条件）的误差函数；w1、w2为对应的权重系数。
Legendre正交多项式自由曲面同样也可以通过控制孔径边缘处（对应u=±1以及v=±1）曲面同基底曲面间的矢高差之和为0，对曲面整体的矢高差进行控制，其方法与前述Chebyshev多项式自由曲面的约束方法相同。对于前六阶多项式，经过积分计算得到Legendre正交多项式自由曲面孔径边缘处矢高差之和与系数关系为：
$$ \begin{split} zsag{|_{v = 1}} =& 2{\alpha _{{\text{0,0}}}} + 2\sqrt 5 {\alpha _{{\text{0,2}}}} + 2\sqrt 7 {\alpha _{{\text{0,3}}}} + 6{\alpha _{{\text{0,4}}}} + 2\sqrt {11} {\alpha _{{\text{0,5}}}} + \\ & 2\sqrt {13} {\alpha _{{\text{0,6}}}} \\ zsag{|_{v = - 1}} =& 2{\alpha _{{\text{0,0}}}} + 2\sqrt 5 {\alpha _{{\text{0,2}}}} - 2\sqrt 7 {\alpha _{{\text{0,3}}}} + 6{\alpha _{{\text{0,4}}}} -\\ & 2\sqrt {11} {\alpha _{{\text{0,5}}}} + 2\sqrt {13} {\alpha _{{\text{0,6}}}} \\ zsag{|_{u = 1}} =& 2{\alpha _{{\text{0,0}}}} + 2\sqrt 5 {\alpha _{{\text{2,0}}}} + 6{\alpha _{{\text{4,0}}}} + 2\sqrt {13} {\alpha _{{\text{6,0}}}} \\ zsag{|_{u = - 1}} = & 2{\alpha _{{\text{0,0}}}} + 2\sqrt 5 {\alpha _{{\text{2,0}}}} + 6{\alpha _{{\text{4,0}}}} + 2\sqrt {13} {\alpha _{{\text{6,0}}}} \\ zsa{g_{{\text{sum}}}} =& 8{\alpha _{{\text{0,0}}}} + 4\sqrt 5 ({\alpha _{{\text{2,0}}}} + {\alpha _{{\text{0,2}}}}) + 12({\alpha _{4,0}} + {\alpha _{0,4}}) +\\ & 4\sqrt {13} ({\alpha _{6,0}} + {\alpha _{0,6}}) \\[-10pt] \end{split} $$ (17) 约束zsagsum=0使孔径边缘处曲面同基底面间矢高差之和为0。同时，也需要添加系数线性组合等于0的约束，从而消除由多项式自身带来的piston项以及tilt项，如公式（18）所示：
$$ \begin{split} {\text{piston}} =& {\alpha _{{\text{0,0}}}} - \frac{{\sqrt 5 }}{2}{\alpha _{{\text{2,0}}}} - \frac{{\sqrt 5 }}{2}{\alpha _{{\text{0,2}}}} + \frac{9}{8}{\alpha _{{\text{4,0}}}} + \frac{5}{4}{\alpha _{{\text{2,2}}}} + \frac{9}{8}{\alpha _{{\text{0,4}}}} -\\ & \frac{{{\text{5}}\sqrt {{\text{13}}} }}{{{\text{16}}}}{\alpha _{{\text{6,0}}}} - \frac{{9\sqrt {\text{5}} }}{{{\text{16}}}}{\alpha _{{\text{4,2}}}} - \frac{{9\sqrt {\text{5}} }}{{{\text{16}}}}{\alpha _{{\text{2,4}}}} - \frac{{{\text{5}}\sqrt {{\text{13}}} }}{{{\text{16}}}}{\alpha _{{\text{0,6}}}} = 0 \\ {\text{tilt}} =& \sqrt 3 {\alpha _{{\text{0,1}}}} - \frac{{\sqrt {15} }}{2}{\alpha _{{\text{2,1}}}} - \frac{{3\sqrt 7 }}{2}{\alpha _{{\text{0,3}}}}{\text{ + }}\frac{{{\text{9}}\sqrt {\text{3}} }}{2}{\alpha _{{\text{4,1}}}}{\text{ + }}\\ & \frac{{{\text{3}}\sqrt {{\text{35}}} }}{{\text{4}}}{\alpha _{{\text{2,3}}}}{\text{ + }}\frac{{{\text{15}}\sqrt {{\text{11}}} }}{{\text{8}}}{\alpha _{{\text{0,5}}}} = 0 \\[-10pt] \end{split} $$ (18) 在曲面关于YOZ平面对称的前提下，关于u的奇数阶项同样也不能使用。
-
为验证前述使用Chebyshev多项式自由曲面面型的设计方法的有效性，设计了一个离轴三反系统实例。系统有5°×4°的矩形视场，F数为2.5，焦距100 mm，工作波段为长波红外（8~12 μm）。该系统的主镜和三镜实际上是同一个曲面，采用相同的曲面表达式，即主镜和三镜是同一个镜子的不同区域。如此的多面共体设计方案可以大大降低系统的装调难度，同时，相对于将多个采用不同面形表达式的曲面进行共体加工的方案，该设计方案可以有效降低系统的加工与检测难度和成本。同时设计了使用XY多项式自由曲面和Chebyshev多项式自由曲面的两个系统进行对比。两种面形描述中都包含一个二次曲面基底，多项式部分均用到4阶。系统的孔径光阑位于系统最前端，系统中的主三镜以及次镜均使用矩形孔径。在使用XY多项式的系统设计中，并未控制曲面和基底二次曲面的矢高差。在使用Chebyshev多项式自由曲面系统的优化过程中添加相应的边缘矢高差和为0、以及曲面piston和tilt项为0的约束条件。对于两个系统设计，通过ABCD矩阵计算并控制系统的焦距，通过实际光线追迹数据计算系统畸变并进行控制。在系统优化过程中，每个曲面的孔径大小是动态变化的。在光学设计软件使用的Chebyshev多项式和Legendre多项式自由曲面的描述中，用于归一化的x和y方向的孔径大小均为面形描述的其中一个参数，且被设为优化变量。在系统优化过程中，通过选择特定的边缘视场、边缘孔径光线并进行实际光线追迹，可以得到每个曲面实际在x和y方向的孔径大小。然后约束曲面描述中的孔径大小和追迹得到的结果相等，即可以保证曲面描述中的归一化孔径的准确性，并保证设计结果与约束条件使用的准确性。经过优化后，两个系统的光路图如图2(a)和2(b)所示。系统的调制传递函数（MTF）曲线以及全视场RMS波像差如图3所示。对两个系统的共体主三镜以及次镜进行了曲面同基底曲面间的矢高差PV值（sag difference PV, SDPV）以及最大法向偏差（maximum normal deviation, MND）分析，同时还给出了系统的像质（全视场平均RMS波像差，RMS WFE，λ=10000 nm），如表3所示。可以看出，主三镜以及次镜使用Chebyshev多项式自由曲面面型后，与使用XY多项式自由曲面面型相比，像质并未发生明显下降，但曲面同基底面间的矢高差明显减小，曲面面形的检测难度下降。图4列举了两个系统中各个反射面上曲面同基底面间的矢高差图。以上说明了采用文中提出的方法在矩形孔径曲面应用Chebyshev多项式自由曲面面型进行矢高差控制与系统设计的有效性。
图 2 设计实例A的光路图。(a) 采用XY多项式自由曲面的系统；(b) 采用Chebyshev多项式自由曲面的系统；(c) 采用Legendre多项式自由曲面并同时添加两类约束条件优化后的系统
Figure 2. System layout for design example A. (a) System using XY polynomials surface; (b) System using Chebyshev polynomials surface; (c) System using Legendre polynomials surface and using two types of constraints during optimization
图 3 实例A采用XY多项式自由曲面和Chebyshev多项式自由曲面面型后的MTF曲线(a)以及全视场RMS波像差(b)
Figure 3. MTF (a) and full FOV RMS wavefront error (b) of systems in example A using XY polynomials and Chebyshev polynomials surface types
表 3 设计实例A的采用XY多项式自由曲面和Chebyshev多项式自由曲面的曲面矢高差对比和像质
Table 3. Surface sag difference and imaging performance for design example A using XY polynomials and Chebyshev polynomials surface types
Surface type XY polynomials Chebyshev polynomials Constraints None Sag difference on aperture margins SDPV/mm MND/(°) SDPV/mm MND/(°) M1 0.667 0.494 0.090 0.090 M2 0.580 2.368 0.254 0.940 Sum 1.247 2.862 0.344 1.030 RMS WFE 0.021λ 0.021λ 
图 4 实例A采用XY多项式自由曲面和Chebyshev多项式自由曲面面型后各曲面同基底曲面矢高差图
Figure 4. Sag difference between the freeform surface and base surface for the surfaces in example A using XY polynomials and Chebyshev polynomials surface types
-
为验证前述使用Legendre多项式自由曲面面型设计方法的有效性，设计了三个离轴三反系统实例，均首先采用XY多项式自由曲面进行设计。使用了二次曲面基底，但不添加有关于矢高差的约束，然后将其转换成Legendre多项式自由曲面后再进一步设计。由于Legendre多项式各项系数和XY多项式各项系数之间有线性关系，可以直接通过线性变换实现面型转换。所有设计实例中，XY多项式和Legendre多项式均只使用到四阶。由于光学设计软件CODE V中没有Legendre正交多项式面型，因此需要在CODE V中采用用户自定义面型（user defined surface，UDS）进行编译。优化过程中，在评价函数中分别添加矩形孔径边缘处曲面同基底曲面间矢高差之和的约束、系数平方和误差函数，以及同时使用以上两种约束条件。在优化过程中同时添加曲面piston和tilt项为0的约束。通过分析曲面同基底面的最大法向偏离、矢高偏差PV值，以及系统的像质（全视场平均RMS波像差）验证各项约束条件对曲面检测难度的约束效果。
设计实例A同前述例子相同，为主三镜采用同一曲面表达式的共体自由曲面离轴三反系统。采用Legendre多项式自由曲面设计得到的系统如图2(c)所示。采用XY多项式自由曲面以及Legendre多项式自由曲面（不同约束条件）的各系统的MTF曲线以及全视场RMS波像差如图5所示，各系统的像质较为接近。对于实例A（包括采用Chebyshev多项式自由曲面的设计结果），各系统的径向畸变和切向畸变均分别控制在0.35%和0.75%之内。采用不同约束条件的系统设计结果对比列于表4 （λ=10000 nm）。使用XY多项式自由曲面，曲面同基底面间的矢高差PV值以及最大法向偏离均较大。而当将曲面替换为Legendre正交多项式并添加相关约束进行优化后，在保证像质基本一致的前提下，反射面上曲面同基底面间的矢高差PV值以及最大法向偏差明显变小。图6列举了应用Legendre多项式自由曲面后系统中各个反射面同基底曲面间的矢高差图。
图 5 实例A采用XY多项式自由曲面和Legendre多项式自由曲面面型后的MTF曲线（a）以及全视场RMS波像差（b）
Figure 5. MTF (a) and full FOV RMS wavefront error (b) of systems in example A using XY polynomials and Legendre polynomials surface types
表 4 设计实例A的采用XY多项式自由曲面和Legendre多项式自由曲面的曲面矢高差对比和像质
Table 4. Surface sag difference and imaging performance for design example A using XY polynomials and Legendre polynomials surface types
Surface type XY polynomials Legendre polynomials Constraints None Sag difference on aperture margins Square sum of surface coefficients Both types of constraints SDPV/mm MND/(°) SDPV/mm MND/(°) SDPV/mm MND/(°) SDPV/mm MND/(°) M1 0.667 0.494 0.097 0.100 0.100 0.112 0.097 0.097 M2 0.580 2.368 0.156 0.710 0.156 0.601 0.156 0.747 Sum 1.247 2.862 0.253 0.810 0.256 0.713 0.253 0.844 RMS WFE 0.021λ 0.020λ 0.020λ 0.020λ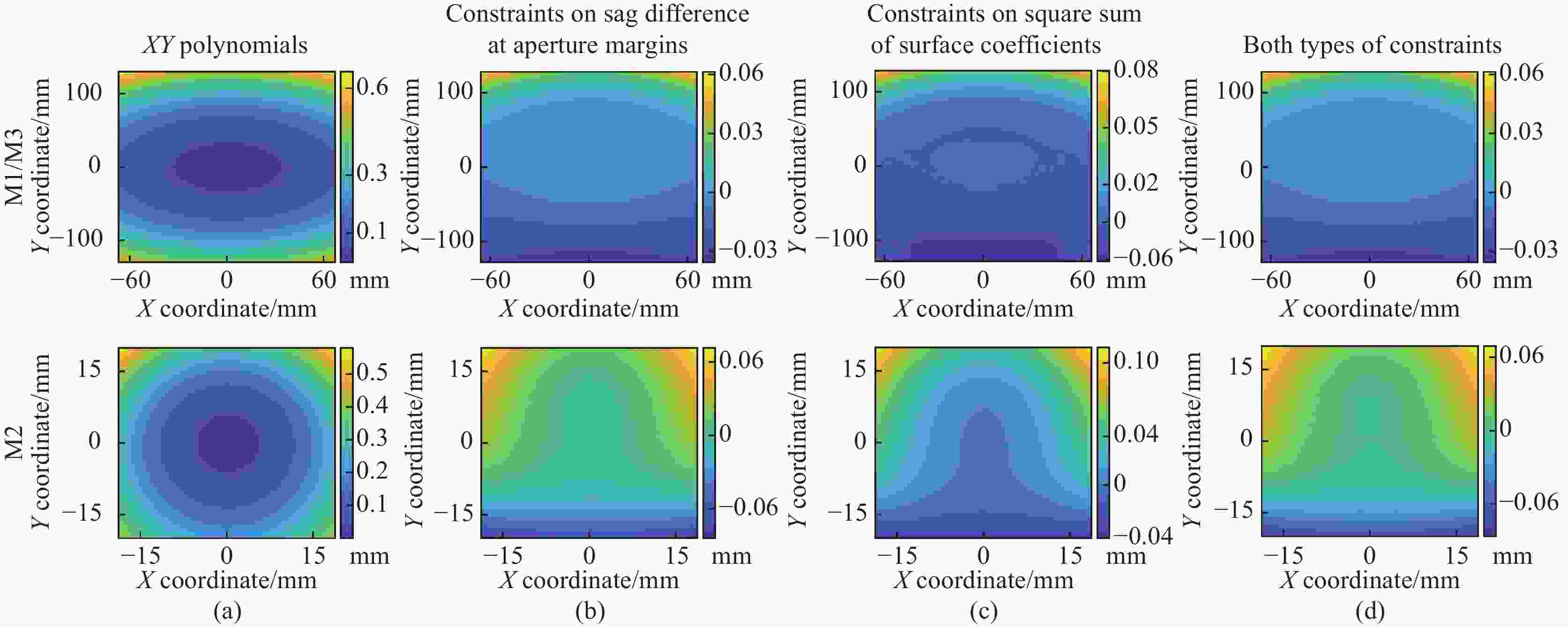 
图 6 实例A采用XY多项式自由曲面和Legendre多项式自由曲面面型后各曲面同基底曲面矢高差图
Figure 6. Sag difference between the freeform surface and base surface for the surfaces in example A using XY polynomials and Legendre polynomials surface types
设计实例B为传统zig-zag结构的离轴三反系统。采用8°×6°矩形视场，F数为1.9，焦距57 mm，工作波段为长波红外（8~12 μm）。次镜为圆形的孔径光阑，面型始终使用XY多项式自由曲面。采用XY多项式自由曲面和Legendre多项式自由曲面设计得到的系统如图7所示。各系统的MTF曲线以及全视场RMS波像差如图8所示，其结果较为接近。各系统的径向畸变和切向畸变均分别控制在1%和1.5%之内。系统设计结果对比列于表5（λ=10000 nm）。使用XY多项式自由曲面，曲面同基底面间的矢高差PV值以及最大法向偏离均较大。而当将曲面替换为Legendre正交多项式并添加相关约束进行优化后，在保证像质基本一致的前提下，反射面上曲面同基底面间的矢高差PV值以及最大法向偏差明显变小。在同时添加孔径边缘矢高差之和以及系数平方和约束条件后，系统整体加工检测难度改善效果最佳。图9列举了各类约束下系统主镜与三镜曲面同基底曲面间的矢高差图。
图 7 设计实例B的光路图。(a) 采用XY多项式自由曲面的系统；(b)采用Legendre多项式自由曲面并同时添加两类约束条件优化后的系统
Figure 7. System layout for design example B. (a) System using XY polynomials surface type; (b) System using Legendre polynomials surface type and using two types of constraints during optimization
图 8 实例B采用XY多项式自由曲面和Legendre多项式自由曲面面型后的MTF曲线以及全视场RMS波像差
Figure 8. MTF and full FOV RMS wavefront error of systems in example B using XY polynomials and Legendre polynomials surface types
表 5 设计实例B的采用XY多项式自由曲面和Legendre多项式自由曲面的曲面矢高差对比和像质
Table 5. Surface sag difference and imaging performance for design example B using XY polynomials and Legendre polynomials surface types
Surface type XY polynomials Legendre polynomials Constraints None Sag difference on aperture margins Square sum of surface coefficients Both types of constraints SDPV/mm MND/(°) SDPV/mm MND/(°) SDPV/mm MND/(°) SDPV/mm MND/(°) M1 1.759 5.259 0.116 0.381 0.170 0.681 0.108 0.360 M3 0.860 1.339 0.219 0.447 0.209 0.428 0.216 0.436 Sum 2.619 6.598 0.335 0.828 0.379 1.109 0.324 0.796 RMS WFE 0.008λ 0.008λ 0.008λ 0.008λ 
图 9 实例B采用XY多项式自由曲面和Legendre多项式自由曲面面型后各曲面同基底曲面矢高差图
Figure 9. Sag difference between the freeform surface and base surface for the surfaces in example B using XY polynomials and Legendre polynomials surface types
设计实例C为共体离轴三反系统，采用一种特殊的紧凑型柱形轮廓结构，系统F数为3，入瞳直径92 mm，视场角2°×1.6°，工作波长为中波红外（3~5 μm）。系统在像面前有一个实出瞳，即系统的孔径光阑。系统内部有一个中间像面。采用XY多项式自由曲面和Legendre多项式自由曲面设计得到的系统如图10所示，各系统的MTF曲线以及全视场RMS波像差如图11所示。各系统的径向畸变和切向畸变均分别控制在2.5%和1.5%之内。系统设计结果对比列于表6（λ=4000 nm）。使用XY多项式自由曲面，曲面同基底面间的矢高差PV值以及最大法向偏离均较大。而当将曲面替换为Legendre正交多项式并添加相关约束进行优化后，在保证像质基本一致的前提下，反射面上曲面同基底面间的矢高差PV值以及最大法向偏差明显变小。在同时添加孔径边缘矢高差之和以及系数平方和约束条件后，系统加工检测难度整体上改善效果最佳。图12列举了XY多项式系统和应用Legendre面型并分别添加三类约束后系统各个曲面同基底曲面间矢高差图。
以上三个设计实例结果表明，基于Legendre多项式自由曲面的数学性质，采用文中提到的三类约束（采用孔径边缘矢高差之和约束、系数平方和约束以及同时采用两种约束）都可以对自由曲面和基底曲面的矢高差实现较好的控制。单独使用孔径边缘矢高差之和的约束与单独使用系数平方和约束，两者的效果接近。而从整体来看，同时采用以上两类约束后，矢高差和最大法向偏差降低最为明显，系统加工检测难度整体上改善效果最佳，工艺性最好。
图 10 设计实例C的光路图。(a) 采用XY多项式自由曲面的系统；(b)采用Legendre多项式自由曲面并同时添加两类约束条件优化后的系统
Figure 10. System layout for design example C. (a) System using XY polynomials surface type; (b) System using Legendre polynomials surface type and using two types of constraints during optimization
图 11 实例C采用XY多项式自由曲面和Legendre多项式自由曲面面型后的MTF曲线(a)以及全视场RMS波像差(b)
Figure 11. MTF (a) and full FOV RMS wavefront error (b) of systems in example C using XY polynomials and Legendre polynomials surface types
表 6 设计实例C的采用XY多项式自由曲面和Legendre多项式自由曲面的曲面矢高差对比和像质
Table 6. Surface sag difference and imaging performance for design example C using XY polynomials and Legendre polynomials surface types
Surface type XY polynomials Legendre polynomials Constraints None Sag difference on aperture margins Square sum of surface coefficients Both types of constraints SDPV/mm MND/(°) SDPV/mm MND/(°) SDPV/mm MND/(°) SDPV/mm MND/(°) M1 1.941 2.013 1.979 1.874 1.851 2.061 1.734 1.373 M2 0.900 7.600 0.033 0.585 0.050 1.078 0.033 0.591 M3 6.525 5.070 0.645 0.536 0.500 0.448 0.540 0.457 Sum 9.366 14.683 2.657 2.995 2.401 3.587 2.307 2.421 RMS WFE 0.047λ 0.050λ 0.045λ 0.051λ 
图 12 实例C采用XY多项式自由曲面和Legendre多项式自由曲面面型后各曲面同基底曲面矢高差图
Figure 12. Sag difference between the freeform surface and base surface for the surfaces in example C using XY polynomials and Legendre polynomials surface types
如引言中所述，采用传统的XY多项式自由曲面进行自由曲面系统设计，也可以进行矢高差大小的控制；而XY多项式的各项系数经过线性变换后，可以直接解析地转化成Chebyshev多项式和Legendre多项式的系数，系统设计自由度也未发生变化。因此，采用XY多项式自由曲面可以达到和使用Chebyshev多项式和Legendre多项式自由曲面系统类似或者相同的效果。但是，由于XY多项式自由曲面没有正交性，一般需要通过选取曲面上大量离散的特征点，计算特征点处的曲面矢高和基底曲面间的矢高差并进行控制。如果特征点的数量较多，则系统优化速度较慢，效率低。而使用文中采用的方域正交多项式自由曲面则可以利用其正交性（例如基于系数平方和的约束），较为容易、高效、简洁地实现矢高差控制，进而实现自由曲面的可检测性实时估计，基本不会减慢优化设计过程。因此，文中设计得到的使用XY多项式曲面的对比系统均未对矢高差进行控制，以此来体现光学设计过程中（包括使用正交多项式曲面的系统），在未加入任何矢高差约束时，系统实际面形和基底面形可能出现的偏离较大的情况（甚至出现较大的回转对称分量）。如果不对Chebyshev多项式和Legendre多项式施加约束，其设计结果与采用XY多项式自由曲面的系统设计结果趋于类似。而采用相应约束后，在基本不牺牲像质的前提下，曲面矢高差可以得到非常有效且高效的控制。
-
在设计自由曲面成像系统过程中，除了要尽可能地提升系统的成像质量，还应该实现良好的工艺性。为了使自由曲面利于进行高精度的干涉检测（例如采用计算全息方法），自由曲面同基底曲面的矢高差应该尽量小。文中针对自由曲面系统中常见的矩形曲面孔径，研究了基于方域正交的Chebyshev多项式和Legendre多项式的自由曲面成像系统设计方法。根据两种面型的数学表达式以及其性质，推导出基于孔径边缘矢高差控制以及系数平方和控制的相关数学约束方法，可以实现有效且高效地控制矩形孔径自由曲面相对于基底曲面的矢高差，降低曲面的检测难度并提高工艺性。通过多个设计实例验证了提出方法的有效性。该方法可以用于各类自由曲面系统的设计与研制。同时，该方法易于在光学设计软件以及其他优化与计算平台和环境进行使用。后续工作将继续研究其他类型的正交多项式在各类系统设计中的应用。
Design method of imaging systems using square-domain orthogonal polynomials freeform surface (invited)
-
摘要: 自由曲面为光学系统设计带来了新的设计自由度，可以实现性能与参数更高、结构更紧凑的系统，但自由曲面的加工与检测难度较大，应在设计过程中对工艺性进行实时表征与控制。使用正交多项式面型可以较为容易地实现自由曲面同基底曲面矢高差的控制，但目前常用的大多是在圆域内正交的多项式，对于自由曲面离轴非对称系统中曲面常用的矩形孔径或者方形孔径局限性较大。针对以上问题，提出了采用方域内具有正交特性的二维Chebyshev多项式以及二维Legendre多项式进行自由曲面成像系统设计的方法。提出采用正交多项式孔径边缘积分的约束方法，以及采用控制方域正交多项式系数平方和的方法，配合正交多项式系数的其他线性约束，在不明显降低系统成像质量的情况下，实现高效的自由曲面系统设计以及曲面检测难度的实时表征与控制。通过多个不同结构的自由曲面成像系统设计实例，说明了所提出的设计方法的可行性与效果。所提出的方法为常用的有矩形曲面孔径的自由曲面系统设计提供了新思路，可以有效提升整个自由曲面系统研制过程的效率。Abstract:
Objective Compared with traditional spherical and aspherical optical surfaces, freeform optical surface offers more degrees of design freedom, and it can be used in the design of imaging systems with more advanced system specifications, better imaging performance, more compact structure and novel functions. During freeform imaging system design and optimization, high imaging performance is an important design target. In addition, the freeform surfaces should be easier to be tested and fabricated. Interferometric surface testing is one of the most accurate methods for freeform surface and it is now increasingly used. To decrease the testing difficulty, the sag difference between the freeform surface and the base sphere or base conic should be as small as possible. For rotationally symmetric systems, the sag difference can be controlled easily and efficiently by using circular-domain orthogonal polynomial surfaces such as Zernike polynomials surface and Q2D polynomials surface. However, for nonrotationally symmetric freeform systems, as rectangular field-of-view is often used, the freeform surfaces often have rectangular aperture, the ability of circular-domain orthogonal polynomial surfaces is limited. Therefore, it is necessary to establish a design method to control the testing difficulty of freeform surface with rectangular aperture. Methods A design method of imaging systems using square-domain orthogonal polynomials freeform surface is proposed. Two kinds of square-domain orthogonal polynomials of Chebyshev polynomials and Legendre polynomials are analyzed and used. The inner product of the surface sag difference using orthogonal surfaces is related to the weighted square sum of the polynomial coefficients. For Chebyshev polynomials, as its weight function is a complicated function of x and y, it is not straightforward to use this property to control the sag difference. However, the sag difference can be controlled by constraining the sum of sag difference around the margins of the rectangular aperture to be zero. In addition, piston and tilt terms in orthogonal surface description should be zero. This can be controlled by constraining linear combinations of surface coefficients to be zero during optimization. For Legendre polynomials surface type, the constraint on the aperture margin can still be used. In addition, as the weight function of Legendre polynomials is one, the square sum of the polynomial coefficients can be used directly, which can be integrated into the total merit function during optimization. Detailed mathematical equations for establishing the design constraints and merit functions can be found in Eqs. (8), (9), (15)-(18). Results and Discussions Several design examples are used to show the feasibility and effect of the proposed design method. For Chebyshev polynomials freeform surface, a freeform off-axis three-mirror system whose primary and tertiary mirrors are integrated into one surface is designed. Compared with the design using traditional XY polynomials surface without sag difference constraints, the sag difference of the freeform surfaces in the system using Chebyshev polynomials surface is effectively controlled (Fig.2-3, Tab.3). For Legendre polynomials freeform surface, three kinds of off-axis three-mirror systems are designed: a system whose primary and tertiary mirrors are integrated into one surface, a system with the traditional zig-zag structure, and a system with a cylindrical package and real exit pupil. The design constraints on the sag difference at aperture margins, and the constraints on square sum of surface coefficients are used. Compared with the design using traditional XY polynomials surface without sag difference constraints, the sag difference of the freeform surfaces in the system using Legendre polynomials surface is effectively controlled (Fig.4, Fig.6, Fig.8, Tab.4-6). Conclusions For the commonly used rectangular surface aperture in freeform imaging system, a design method of freeform imaging system using square-domain orthogonal polynomials freeform surface is proposed. Chebyshev polynomials freeform surface and Legendre polynomials freeform surfaces are used and discussed. Based on the mathematical properties of the two kinds of polynomials, the mathematical constraints on the sag difference at the margins of the rectangular aperture and the constraints on the square sum of the polynomial coefficients are derived. Several design examples are given to show the feasibility and effect of the proposed design method. The design results show that, using the proposed design method and square-domain orthogonal Chebyshev and Legendre polynomials, the surface sag difference between the freeform surface and the base surface can be reduced effectively, and the testing difficulty can be reduced. The proposed method can be used in the design and development of all kinds of freeform imaging systems, and can be easily implemented in optical design software and other computing platforms and environments. -
图 2 设计实例A的光路图。(a) 采用XY多项式自由曲面的系统；(b) 采用Chebyshev多项式自由曲面的系统；(c) 采用Legendre多项式自由曲面并同时添加两类约束条件优化后的系统
Figure 2. System layout for design example A. (a) System using XY polynomials surface; (b) System using Chebyshev polynomials surface; (c) System using Legendre polynomials surface and using two types of constraints during optimization
图 3 实例A采用XY多项式自由曲面和Chebyshev多项式自由曲面面型后的MTF曲线(a)以及全视场RMS波像差(b)
Figure 3. MTF (a) and full FOV RMS wavefront error (b) of systems in example A using XY polynomials and Chebyshev polynomials surface types
图 4 实例A采用XY多项式自由曲面和Chebyshev多项式自由曲面面型后各曲面同基底曲面矢高差图
Figure 4. Sag difference between the freeform surface and base surface for the surfaces in example A using XY polynomials and Chebyshev polynomials surface types
图 5 实例A采用XY多项式自由曲面和Legendre多项式自由曲面面型后的MTF曲线（a）以及全视场RMS波像差（b）
Figure 5. MTF (a) and full FOV RMS wavefront error (b) of systems in example A using XY polynomials and Legendre polynomials surface types
图 6 实例A采用XY多项式自由曲面和Legendre多项式自由曲面面型后各曲面同基底曲面矢高差图
Figure 6. Sag difference between the freeform surface and base surface for the surfaces in example A using XY polynomials and Legendre polynomials surface types
图 7 设计实例B的光路图。(a) 采用XY多项式自由曲面的系统；(b)采用Legendre多项式自由曲面并同时添加两类约束条件优化后的系统
Figure 7. System layout for design example B. (a) System using XY polynomials surface type; (b) System using Legendre polynomials surface type and using two types of constraints during optimization
图 8 实例B采用XY多项式自由曲面和Legendre多项式自由曲面面型后的MTF曲线以及全视场RMS波像差
Figure 8. MTF and full FOV RMS wavefront error of systems in example B using XY polynomials and Legendre polynomials surface types
图 9 实例B采用XY多项式自由曲面和Legendre多项式自由曲面面型后各曲面同基底曲面矢高差图
Figure 9. Sag difference between the freeform surface and base surface for the surfaces in example B using XY polynomials and Legendre polynomials surface types
图 10 设计实例C的光路图。(a) 采用XY多项式自由曲面的系统；(b)采用Legendre多项式自由曲面并同时添加两类约束条件优化后的系统
Figure 10. System layout for design example C. (a) System using XY polynomials surface type; (b) System using Legendre polynomials surface type and using two types of constraints during optimization
图 11 实例C采用XY多项式自由曲面和Legendre多项式自由曲面面型后的MTF曲线(a)以及全视场RMS波像差(b)
Figure 11. MTF (a) and full FOV RMS wavefront error (b) of systems in example C using XY polynomials and Legendre polynomials surface types
图 12 实例C采用XY多项式自由曲面和Legendre多项式自由曲面面型后各曲面同基底曲面矢高差图
Figure 12. Sag difference between the freeform surface and base surface for the surfaces in example C using XY polynomials and Legendre polynomials surface types
表 1 前六阶一维Chebyshev多项式
Table 1. 1D Chebyshev polynomial up to the sixth order
n Tn(u) 0 1 1 u 2 2u2−1 3 4u3−3u 4 8u4−8u2+1 5 16u5−20u3+5u 6 32u6−48u4+18u2−1 
下载: 导出CSV
表 2 前六阶一维Legendre多项式
Table 2. 1D Legendre polynomial up to the sixth order
n Pn(u) 0 1 1 $\sqrt {\text{3}} u$ 2 $(\sqrt {\text{5}} {\text{/2)(3}}{u^2} - 1)$ 3 $(\sqrt {\text{7}} {\text{/2)(5}}{u^{\text{3}}} - {\text{3}}u)$ 4 $({\text{3/8)(35}}{u^{\text{4}}} - {\text{30}}{u^2} + 3)$ 5 $(\sqrt {11} {\text{/8)(63}}{u^{\text{5}}} - {\text{70}}{u^3} + 15 u)$ 6 $(\sqrt {1{\text{3}}} {\text{/16)(231}}{u^{\text{6}}} - {\text{315}}{u^{\text{4}}} + 1{\text{0}}5{u^{\text{2}}} - 5)$
下载: 导出CSV
表 3 设计实例A的采用XY多项式自由曲面和Chebyshev多项式自由曲面的曲面矢高差对比和像质
Table 3. Surface sag difference and imaging performance for design example A using XY polynomials and Chebyshev polynomials surface types
Surface type XY polynomials Chebyshev polynomials Constraints None Sag difference on aperture margins SDPV/mm MND/(°) SDPV/mm MND/(°) M1 0.667 0.494 0.090 0.090 M2 0.580 2.368 0.254 0.940 Sum 1.247 2.862 0.344 1.030 RMS WFE 0.021λ 0.021λ
下载: 导出CSV
表 4 设计实例A的采用XY多项式自由曲面和Legendre多项式自由曲面的曲面矢高差对比和像质
Table 4. Surface sag difference and imaging performance for design example A using XY polynomials and Legendre polynomials surface types
Surface type XY polynomials Legendre polynomials Constraints None Sag difference on aperture margins Square sum of surface coefficients Both types of constraints SDPV/mm MND/(°) SDPV/mm MND/(°) SDPV/mm MND/(°) SDPV/mm MND/(°) M1 0.667 0.494 0.097 0.100 0.100 0.112 0.097 0.097 M2 0.580 2.368 0.156 0.710 0.156 0.601 0.156 0.747 Sum 1.247 2.862 0.253 0.810 0.256 0.713 0.253 0.844 RMS WFE 0.021λ 0.020λ 0.020λ 0.020λ
下载: 导出CSV
表 5 设计实例B的采用XY多项式自由曲面和Legendre多项式自由曲面的曲面矢高差对比和像质
Table 5. Surface sag difference and imaging performance for design example B using XY polynomials and Legendre polynomials surface types
Surface type XY polynomials Legendre polynomials Constraints None Sag difference on aperture margins Square sum of surface coefficients Both types of constraints SDPV/mm MND/(°) SDPV/mm MND/(°) SDPV/mm MND/(°) SDPV/mm MND/(°) M1 1.759 5.259 0.116 0.381 0.170 0.681 0.108 0.360 M3 0.860 1.339 0.219 0.447 0.209 0.428 0.216 0.436 Sum 2.619 6.598 0.335 0.828 0.379 1.109 0.324 0.796 RMS WFE 0.008λ 0.008λ 0.008λ 0.008λ
下载: 导出CSV
表 6 设计实例C的采用XY多项式自由曲面和Legendre多项式自由曲面的曲面矢高差对比和像质
Table 6. Surface sag difference and imaging performance for design example C using XY polynomials and Legendre polynomials surface types
Surface type XY polynomials Legendre polynomials Constraints None Sag difference on aperture margins Square sum of surface coefficients Both types of constraints SDPV/mm MND/(°) SDPV/mm MND/(°) SDPV/mm MND/(°) SDPV/mm MND/(°) M1 1.941 2.013 1.979 1.874 1.851 2.061 1.734 1.373 M2 0.900 7.600 0.033 0.585 0.050 1.078 0.033 0.591 M3 6.525 5.070 0.645 0.536 0.500 0.448 0.540 0.457 Sum 9.366 14.683 2.657 2.995 2.401 3.587 2.307 2.421 RMS WFE 0.047λ 0.050λ 0.045λ 0.051λ
下载: 导出CSV
-
[1] 杨通, 段璎哲, 程德文, 等. 自由曲面成像光学系统设计: 理论、发展与应用[J]. 光学学报, 2021, 41(1): 0108001. doi: 10.3788/AOS202141.0108001 Yang Tong, Duan Yingzhe, Cheng Dewen, et al. Freeform imaging optical system design: Theories, development and application [J]. Acta Optica Sinica, 2021, 41(1): 0108001. (in Chinese) doi: 10.3788/AOS202141.0108001 [2] Wu R, Feng Z, Zheng Z, et al. Design of freeform illumination optics [J]. Laser & Photonics Reviews, 2018, 12(7): 1700310. [3] 许宁晏, 陈露, 黄静, 等. 自由曲面成像光学系统的初始结构设计方法[J]. 红外与激光工程, 2022, 51(2): 20210852. doi: 10.3788/IRLA20210852 Xu Ningyan, Chen Lu, Huang Jing, et al. Review of design methodology for starting-point of freeform surface imaging optical system [J]. Infrared and Laser Engineering, 2022, 51(2): 20210852. (in Chinese) doi: 10.3788/IRLA20210852 [4] Wills S. Freeform optics: notes from the revolution [J]. Optics and Photonics News, 2017, 28(7): 34-41. doi: 10.1364/OPN.28.7.000034 [5] 孟庆宇, 汪洪源, 王严, 等. 大线视场自由曲面离轴三反光学系统设计[J]. 红外与激光工程. 2016, 45(10): 1018002. doi: 10.3788/IRLA20164510.1018002 Meng Qingyu, Wang Hongyuan, Wang Yan, et al. Off axis three mirror freeform optical system with large linear field of view [J]. Infrared and Laser Engineering, 2016, 45(10): 1018002. (in Chinese) doi: 10.3788/IRLA20164510.1018002 [6] Wu W, Jin G, Zhu J. Optical design of the freeform reflective imaging system with wide rectangular FOV and low F-number [J]. Results in Physics, 2019, 15: 102688. doi: 10.1016/j.rinp.2019.102688 [7] Xie Y, Mao X, Li J, et al. Optical design and fabrication of an all-aluminum unobscured two-mirror freeform imaging telescope [J]. Applied Optics, 2020, 59(3): 833-840. doi: 10.1364/AO.379324 [8] 陈炳旭, 廖志远, 操超, 等. 大视场大相对孔径自由曲面成像系统设计[J]. 红外与激光工程, 2020, 49(8): 20200005. doi: 10.3788/IRLA20200005 Chen Bingxu, Liao Zhiyuan, Cao Chao, et al. Design of the freeform imaging system with large field of view and large relative aperture [J]. Infrared and Laser Engineering, 2020, 49(8): 20200005. (in Chinese) doi: 10.3788/IRLA20200005 [9] Cheng D, Wang Q, Liu Y, et al. Design and manufacture AR head-mounted displays: A review and outlook [J]. Light: Advanced Manufacturing, 2021, 2(3): 350-369. [10] Wei S, Fan Z, Zhu Z, et al. Design of a head-up display based on freeform reflective systems for automotive applications [J]. Applied Optics, 2019, 58(7): 1675-1681. doi: 10.1364/AO.58.001675 [11] Zhuang Z, Parent J, Roulet P, et al. Freeform wide-angle camera lens enabling mitigable distortion [J]. Applied Optics, 2022, 61(18): 5449-5456. doi: 10.1364/AO.456127 [12] Reimers J, Bauer A, Thompson K P, et al. Freeform spectrometer enabling increased compactness [J]. Light: Science & Applications, 2017, 6: e17026. [13] Liu Yuxuan, Bauer A, Viard T, et al. Freeform hyperspectral imager design in a CubeSat format [J]. Optics Express, 2021, 29(22): 35915-35928. doi: 10.1364/OE.439530 [14] 毛姗姗, 李艳秋, 刘克, 等. 高数值孔径自由曲面极紫外光刻物镜光学设计[J]. 红外与激光工程, 2019, 48(8): 814002. doi: 10.3788/IRLA201948.0814002 Mao Shanshan, Li Yanqiu, Liu Ke, et al. Optical design of high numerical aperture extreme ultraviolet lithography objective with freeform surfaces [J]. Infrared and Laser Engineering, 2019, 48(8): 0814002. (in Chinese) doi: 10.3788/IRLA201948.0814002 [15] Takaki N, Papa J C, Bauer A, et al. Off-axis conics as base surfaces for freeform optics enable null testability [J]. Optics Express, 2020, 28(8): 10859-10872. doi: 10.1364/OE.389426 [16] Takaki N, Bauer A, Rolland J P. On-the-fly surface manufacturability constraints for freeform optical design enabled by orthogonal polynomials [J]. Optics Express, 2019, 27(5): 6129-6146. [17] Takaki N, Bayer A, Rolland J P. Degeneracy in freeform surfaces described with orthogonal polynomials [J]. Applied Optics, 2018, 57(35): 10348-10354. doi: 10.1364/AO.57.010348 [18] 叶井飞. 光学自由曲面的表征方法与技术研究[D]. 南京理工大学, 2018. Ye Jingfei. Research on the method technique for characterizing freeform optical surfaces[D]. Nanjing: Nanjing University of Science & Technology, 2018. (in Chinese) -
点击查看大图
计量
- 文章访问数: 188
- HTML全文浏览量: 19
- PDF下载量: 71
- 被引次数: 0
