-
在计算机视觉中，多目标跟踪（MOT）具有非常重要的地位，是许多其他应用领域的核心技术之一，诸如自动驾驶、航空航天、交通安全、轨迹分析、机器人导航等[1-2]。多目标跟踪的主要任务是估计目标的位置、维持目标编号，由给定的图像序列产生目标的运动轨迹[3]。近些年来受应用需求驱动，针对人体的运动跟踪十分热门且相对成熟[4-5]。在飞行器位姿估计领域中，往往用飞行器上的球形合作靶标来代替飞行器本身进行轨迹的跟踪与识别[6-7]。但不同于人体跟踪，飞行器具有外观相似、遮挡严重、三维空间内运动复杂等特点。目前，在室内定位过程中，对多飞行器运动的定位主要分为两类，一类是基于靶标点的特殊布局，该类方案的跟踪思路简洁，直接根据特征分类即可实现；一类是靶标点布局无明显区别的条件下，实现多飞行器的三维跟踪，基于该类别的跟踪因无直观的特征信息可以利用。如何在没有明显外观特征信息条件下实现多飞行器三维跟踪是多飞行器运动室内定位中急需解决的问题。
为解决多飞行器跟踪问题，基于检测的跟踪方法是最经典也是目前应用最为普遍的方法。然而在目标稠密、外观相似与运动速度较快的场景中，使用较为困难。为了解决上述问题，Hamid Rezatofighi S等人[8]采用计算联合概率得分策略关联检测与跟踪。该方法对强干扰具有很强的适用性，因而被广泛应用，然而由于该种方法必须要计算关联门内所有带分配检测结果的联合概率，算法复杂度高，因此这种方法难以用于目标数量较多的在线跟踪情况。随后Kim C、Oh S等人通过将多目标跟踪归纳为多维分配问题，提出了另外一种多目标数据关联方式，主要包括多假设跟踪（MHT）与马尔科夫链蒙特卡洛数据关联（MCMCDA）等[9-10]，该类方法可以更进一步地描述高阶的数据关联解空间，提供更好的渐进证明。然而其计算量随着被跟踪目标数目的增加而呈指数增长，虽然采用一些剪枝策略可以提高算法的性能，但如何根据目标特性获取剪枝仍是一大难点。最近基于图基的方法受到了重视[11]，且由于其高效的计算效率与优化寻优特征，但更多适用于离线的多目标跟踪数据关联。
该类方法的本质是将多目标问题简化为单目标跟踪问题，在相应推导过程中运用了贝叶斯滤波方法。相关的滤波算法作为重要环节也在不断的演化与改良中。目前较为常见的滤波算法包括：卡尔曼滤波器（KF）、扩展卡尔曼滤波器（EKF）、粒子滤波器（PF）[12]、不敏卡尔曼滤波器（UKF）[13]等。
文中利用固定在飞行器上的合作靶标运动等价飞行器的运动过程，首先根据多飞行器的运动特点，提出了一种基于位移矢量一致性数据关联方法，并利用贝叶斯滤波框架实现了多飞行器轨迹的跟踪；然后基于飞行器初始位置不会重合的前提下，通过求解轨迹Hankel矩阵的秩，缩小相似轨迹判断范围，接着利用Hausdorff距离识别所有待识别的轨迹，注册每一个飞行器的轨迹编号。实验证明，该方法能够较好地完成对多飞行器目标的轨迹跟踪与识别。
-
在线多目标跟踪是指利用过去时刻的信息进行多个目标的跟踪，主要过程如图1所示。如果飞行器运动用刚体运动进行描述，则基于图像序列的多飞行器跟踪问题可表述为，如何从某一时刻的三维观测集合中寻找飞行器上合作靶标点的运动轨迹，并对其进行识别，使得被识别的轨迹分别属于相同的飞行器。
图 1 基于位移矢量一致的飞行器三维跟踪示意图
Figure 1. Schematic diagram of three-dimensional aircraft tracking based on consistent displacement vector
由于多飞行器上合作靶标点跟踪普遍具有目标外观相似、目标数量多、相互之间存在遮挡且频繁交互的特点，其三维跟踪效果很容易受到目标之间相互遮挡的影响，当目标相互靠近时，所得到测量和物体之间的对应关系将难以确定，采用传统的独立跟踪算法对每个目标进行轨迹跟踪，最终他们的轨迹都将被一个最佳测量所吸引，从而合并为一个运动轨迹，出现轨迹劫持等问题。因而，此时存在特征在时间上的匹配问题，即数据关联问题。另一方面对于具有相似外观的多个合作靶标，即使是摄像机都已标定，且在时空上都保持一致的情况下，由于匹配所依赖的光照度一致性假设在此问题中并不适用，而导致匹配的准确性难以保证，因此如何实现相似外观的多飞行器在不同摄像机上的空间匹配也是实现多飞行器运动估计的关键，即多飞行器间的轨迹识别问题。
-
在数据关联领域中，最普遍的方法就是数据关联门限技术。门限是指对跟踪的候选量测定义了一个搜索区域，将门限区域外的量测排除在关联数据外。门限通常被设置在目标的预测位置附近，其大小用残差协方差矩阵
$S\left( t \right)$ 表示。若预测与量测之间的残差矢量$\tilde z\left( t \right)$ 的距离${d^2}$ 在边界为$G$ 的门限内，则允许该量测进行数据关联[14]：$${d^2}\left( t \right) = \tilde z{\left( t \right)^T}{S^{ - 1}}\tilde z\left( t \right) \leqslant G$$ (1) 因为残差
$\tilde z$ 的m维高斯概率密度函数$f$ 为：$$f\left( {\tilde z} \right) = \dfrac{1}{{2{\pi ^{m/2}}\sqrt {\det \left( S \right)} }}\exp \left( { - {d^2}/2} \right)$$ (2) 式中：门限
$G$ 表示一个由多个高斯分布相交形成的超平面的边界。对于三维跟踪，其确认门限为一个椭球体。范数${d^2}$ 假设为卡方分布，其自由度是由量测的维数所决定。 -
全局最邻近标准滤波数据关联算法（GNNSDA）的基本思想是：对于落入门限内的所有量测，计算其与滤波算法预测位置之间的距离，最短者作为目标的轨迹跟踪关联数据[13]。计算时，首先将多目标数据关联问题公式化为一个二维分配问题，然后应用Hungarian算法等方法进行求解。
该方法具有简单、计算速度快和扩展性强的优点，且对于二维分配问题的研究已较为成熟。但在实际应用中，算法对代价矩阵的设计要求高，尤其是当目标空间分布密度高，相互之间遮挡严重时，该算法的误跟踪率高。此外，目标检测算法需维持高检测率和低误检率。当利用贝叶斯递归滤波算法跟踪目标时，一种可选的提高跟踪正确率的方法是增大不确定门限区域的大小，同时考虑门限内所有量测的加权值对贝叶斯滤波预测值进行更新。
-
与GNNSF方法一样，联合概率密度数据关联算法（JPDA）是一种序列跟踪方法，其不同之处在于，贝叶斯滤波预测值的校正是对目标空间分布密度高的应用，该方法是根据不同的线索考虑跟踪门内所有的量测结果。对每一个测量进行加权，获得跟踪的一个可靠测量值[15]。
JPDA算法的目的是求解联合分配事件的条件概率。该算法首先定义一个确认矩阵用来表示所有门限内可行的量测与跟踪的分配。然后通过一定的拆分规则，将确认矩阵拆分得到互联矩阵，来表示每个测量与不同目标匹配的一种可能。根据互联矩阵求得联合事件，依据联合事件即可求解测量与目标关联的概率。
联合概率密度数据关联算法可以处理高密度的多目标跟踪问题，然而其计算量会随着目标数量的增加而呈指数增加，且该方法不能处理目标的起始与终结，所有的测量被用于更新测量误差协方差矩阵可能会使得关联准确率降低，因为不准确的协方差矩阵会导致不准确的门限，因此其门限内的量测数据也将变化。
-
传统的贝叶斯滤波框架下，多目标跟踪问题中最重要的就是数据关联问题，GNNSDA方法在处理一些特殊情况时，效果较差，JPDA方法本身计算复杂度较高。结合飞行器合作靶标的运动特点，对最近邻算法进行改进，将位移矢量一致作为假设条件，可以推导出一种适用于飞行器上合作靶标点跟踪的数据关联技术。
-
设
$k$ 时刻的${N_k}$ 个合作靶标点的状态与${M_k}$ 个合作靶标点的量测分别表示为${{{X}}_k} = \left\{ {{{x}}_k^n,n = 1, \cdots ,{N_k}} \right\}$ 与${{{Z}}_k} = $ $ \left\{ {{{z}}_k^m,m = 1, \cdots ,{M_k}} \right\}$ 。$k$ 时刻的所有累加状态变量与量测量分别表示为${{{X}}^k} = \left\{ {{{{X}}_1}, \cdots ,{{{X}}_k}} \right\}$ 与${{{Z}}^k} = \left\{ {{{{Z}}_1}, \cdots ,{{{Z}}_k}} \right\}$ ，其中$k$ 表示离散采样时间。状态矢量${{{x}}_n}\left( k \right)$ 包含第$n$ 个运动目标的动态信息，如位置与速度。量测包含所有可被直接从图像序列中观测到的位置与噪声。${{{\varLambda }}_{ij}} = 1$ 表示第$i$ 个量测与第$j$ 个目标的状态相关联的事件。利用
${{\varLambda }}$ 定义全体关联事件：$${{\varLambda }} = \left\{ {{{{\varLambda }}_{ij}} \in \left( {0,1} \right)|i = 0, \cdots ,{M_k};j = 1, \cdots ,{N_k}} \right\}$$ (3) 将数据关联问题转化为求解目标状态与量测之间的关联矩阵的问题后，仅需求解：
$${{\varLambda }} = \mathop {\max }\limits_{{\varLambda }} P\left( {{{\varLambda }}|{{{Z}}_k},{{{X}}_k}} \right) = \mathop {\max }\limits_{{\varLambda }} P\left( {{{{Z}}_k}|{{\varLambda }},{{{X}}_k}} \right)P\left( {{{\varLambda }}|{{{X}}_k}} \right)$$ (4) 其中
$P\left( {{{\varLambda }}|{{{X}}_k}} \right)$ 在通常情况下可视为常数。$P\left( {{{{Z}}_k}|{{\varLambda }},{{{X}}_k}} \right)$ 表示状态变量与关联关系已知条件下的量测概率，因此公式（4）可以被化简分解为两部分：一是量测与状态之间的关联为一一对应，一是不对应，因此有：$$\begin{split} {{\varLambda }} =& \arg \mathop {\max }\limits_{{\varLambda }} P\left( {{{{Z}}_k}|{{\varLambda }},{{{X}}_k}} \right) = \\ & \arg \mathop {\max }\limits_{{\varLambda }} \prod\limits_{\left( {i,j} \right) \in {{\varLambda }}} {P\left( {{{Z}}_k^i|{{x}}_k^j} \right)} \\ \end{split} $$ (5) 根据实际多飞行器跟踪的情况，所有量测与目标的组合分配都应该满足如下两个约束条件：
（1）每一个量测最多只分配给一个目标（若为空假设，则
$i = 0$ ）；（2）每一个目标只分配给一个量测。
$$\sum\limits_{j = 1}^{{M_0}} {{{{\varLambda }}_{ij}}} = 1,\sum\limits_{i = 0}^{{N_0}} {{{{\varLambda }}_{ij}} \leqslant 1} $$ (6) 因此，关联矩阵的求解可被转换为求解问题：
$$\begin{split} {{\varLambda }} = \arg \mathop {\max }\limits_{{\varLambda }} \prod\limits_{\left( {i,j} \right) \in {{\varLambda }}} {P\left( {{{Z}}_k^i|{{x}}_k^j} \right)} \\ \;\;\;\;\;\;s.t. \;\;\displaystyle\sum_{j = 1}^{{M_k}} {{{{\varLambda }}_{ij}}} = 1,\displaystyle\sum_{i = 0}^{{N_k}} {{{{\varLambda }}_{ij}} \leqslant 1} \\ \end{split} $$ (7) 因为
$P\left( {{{Z}}_k^i|{{x}}_k^i} \right)$ 表示量测${{Z}}_k^i$ 源自目标${{x}}_k^i$ 的关联概率，所以对于飞行器上的合作靶标点的跟踪有：$$P\left( {{{Z}}_k^i|{{x}}_k^j} \right) = f\left( \cdot \right)$$ (8) 式中：函数
$f$ 表示根据目标动态特性定义的关联概率。若对于每个关联概率
$P\left( {{{Z}}_k^i|{{x}}_k^j} \right)$ 取负对数，则可得公式（9）所示关联代价矩阵：$${{{C}}_{ij}} = - \log P\left( {{{Z}}_k^i|{{x}}_k^j} \right)$$ (9) 为了求得最好的假设，将上述问题数据关联问题公式化为一个二维分配问题。该分配问题的目标函数可以表示为公式（10）所示形式：
$$\begin{split} {{\varLambda }} = \arg \mathop {\min }\limits_{\boldsymbol{\varLambda }} \sum\limits_{i = 0}^{{N_0}} {\sum\limits_{j = 1}^{{M_0}} {{{{C}}_{ij}}{{{\varLambda }}_{ij}}} } \\ s.t. \;\;\displaystyle\sum_{j = 1}^{{M_0}} {{{{\varLambda }}_{ij}}} = 1,\displaystyle\sum_{i = 0}^{{N_0}} {{{{\varLambda }}_{ij}} \leqslant 1} \\ \end{split} $$ (10) 式中：
${{{\varLambda }}_{ij}}$ 是一个表示第$i$ 个变量与第$j$ 个量测之间的二进制变量；${{{C}}_{ij}}$ 为对应关联的代价。通常添加分别空目标与空量测来解释未找到检测或虚假的情况。公式中约束条件强制分配解为唯一的或彻底的（除了空目标与空量测）。对于公式（10），可以利用匈牙利算法、拍卖算法、JVC算法等在多项式复杂度内进行求解。 -
如图2所示，量测与目标之间的关联概率可以通过量测与目标预测之间的距离与速度方向计算。
图 2 目标关联误差矢量定义
Figure 2. Definition of association objects error vector
由距离一致准则，可定义公式函数如下：
$$P_1^i\left( {Z_k^i|x_k^j} \right) = f_1^i\left( {\left\| {Z_k^i - {{H}}x_k^j} \right\|,\sigma _{f1}^2} \right)$$ (11) $${f_n}\left( {x,\sigma _{{f_1}}^2} \right) = \left\{ \begin{array}{l} \exp \left( { - \dfrac{{{x^2}}}{{\sigma _{{f_i}}^2}}} \right)\;\;{\rm{if}}\;{x^2} \leqslant \sigma _{{f_n}}^2,\;n \in {Z^{\rm{ + }}} \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{else}} \\ \end{array} \right.$$ (12) 式中：
$\sigma _{{f_1}}^{}$ 表示数据关联不确定性区域阈值。如图1所示，当类似距离
${d_{63}} = {d_{65}}$ 情况产生时，需要对是哪一个量测进行判断。这时可通过相对位移矢量的方向一致性来判断，即通过量测位移矢量与预测相对位移矢量的夹角大小来描述位移矢量的方向一致性。若假设量测位移矢量为
${{{r}}_1}$ ，预测相对位移矢量为${{{r}}_2}$ ，则根据多目标跟踪问题的描述，由余弦定理有：$$\begin{array}{l} \left| {\nabla {{r}}} \right| = \sqrt {{{\left| {{{{r}}_1}} \right|}^2} + {{\left| {{{{r}}_2}} \right|}^2} - 2\left| {{{{r}}_1}} \right|\left| {{{{r}}_2}} \right|\cos \left( \theta \right)} \\ \;\;\;\;\;\;\;s.t.\;\left| {{{{r}}_1} - {{{r}}_2}} \right| \leqslant \left| {\nabla {{r}}} \right| \leqslant \left| {{{{r}}_1} + {{{r}}_2}} \right| \\ \end{array} $$ (13) 式中：
$0 \leqslant \theta \leqslant 180^\circ $ ，位移矢量一致性描述的夹角可以表示为：$$\theta = \arccos \dfrac{{{{\left| {{{{r}}_1}} \right|}^2} + {{\left| {{{{r}}_2}} \right|}^2} - {{\left| {\nabla {{r}}} \right|}^2}}}{{2{{{r}}_1}{{{r}}_2}}}$$ (14) 所以在位移矢量方向一致性判断准则下，其概率密度函数可以定义为：
$$\left\{ {\begin{array}{*{20}{c}} {P_2^i\left( {Z_k^i|x_k^j} \right) = f_2^i\left( {{\theta _{{{v}}_k^i,{{v}}_k^j}},\sigma _{f2}^2} \right)} \\ {{{v}}_k^i = \overrightarrow {{T_{ij}}} = \left( {Z_{k - 1}^j,{{H}}x_k^i} \right)} \\ {{{v}}_k^j = \overrightarrow {{T_{ij}}} = \left( {Z_{k - 1}^j,{{H}}x_k^i} \right)} \end{array}} \right.$$ (15) 式中：
${\sigma _{f2}}$ 表示关联不确定性区域阈值的大小。此外，一个归一化权值
${w^{\left( i \right)}} > 0$ 表示关联每一个量测的权重，其满足：$$\sum\limits_{i = 1}^{{N_k}} {{w_i}} = 1$$ (16) 因此，概率密度函数
${P_j}\left( {Z_k^i|x_k^i} \right)$ 可以表示为每一个量测的加权和：$${P_1}\left( {Z_k^i|x_k^i} \right) = \sum\limits_{i = 1}^{{M_k}} {w_1^iP_1^i\left( {Z_k^i|x_k^i} \right)} $$ (17) 因此，概率密度函数
$P\left( {Z_k^i|x_k^i} \right)$ 表示如下：$$\begin{split} P\left( {Z_k^i|x_k^i} \right) =& {\lambda _1}{P_1}\left( {Z_k^i|x_k^i} \right) + {\lambda _2}{P_2}\left( {Z_k^i|x_k^i} \right) \\ & s.t.\;{\lambda _1} + {\lambda _2} = 1 \\ \end{split} $$ (18) 在文中设
${\lambda _1} = 0.7$ ，${\lambda _2} = 0.3$ 。相比于GNNSF算法，文中提出的算法可以处理一些特殊的情况，如在目标状态预测门限内具有两个与目标状态预测之间距离相等的量测时，可以利用其速度矢量差进行求解，提高算法的关联精度。
相比于JPDA算法，文中提出的算法对于目标跟踪可以处理目标的起始与终结，而且不需要求解确认矩阵与分解关联矩阵，降低了算法的计算复杂度，大为提高了算法的实际运算速度。
但是需要注意的是，在飞行器运动十分剧烈的情况下，飞行器靶标的位移矢量变化很大，位移矢量一致的假设可能会失效。
-
对飞行器运动进行估计，注册特征点是进行估计的前提。因此文中提出了一种基于动态特性与外观相似的同一飞行器上合作靶标点轨迹的识别方法。其主要包括轨迹粗识别与轨迹细识别两部分。
-
Hankel矩阵是一个每一条副对角线上的元素都相等的方阵。它的作用之一是其秩的大小可以用来描述系统的动态性能[16]。
首先，根据同一飞行器上合作靶标点的轨迹之间具有相似的动态特性，利用三维轨迹离散采样数据构造Hankel矩阵，并比较与验证轨迹之间的动态相似性。若轨迹
$\varGamma$ 是由量测序列$z_k^i$ 组成，其中$s \leqslant k \leqslant e$ ，$s$ 与$e$ 分别表示轨迹的起始与结束时刻。则不同轨迹所具有的动态特性可利用线性回归形式进行表示，因此有：$$ z_{k}^{i}=\sum\limits_{j=1}^{N_{k}} a_{i} z_{k-j}^{i}, k \geq s+N_{k} $$ (19) 对于一个足够大的值
${N_k}$ 。${N_k}$ 表示在无噪声干扰的条件下轨迹所具有的动态特性的复杂度。其中${N_k} = {\rm{rank}}\left( {H_\varGamma ^{\left( m \right)}} \right)$ ，$H_\varGamma ^{\left( m \right)}$ 表示轨迹点所构造的Hankel矩阵，且$m \geqslant n$ 列：$$H_\varGamma ^{\left( m \right)} = \left[ {\begin{array}{*{20}{c}} {z_s^i}&{z_{s + 1}^i}& \cdots &{z_{s + m - 1}^i} \\ {z_{s + 1}^i}&{z_{s + 2}^i}& \cdots &{z_{s + m}^i} \\ \vdots & \vdots & \vdots & \vdots \\ {z_{e - m + 1}^i}&{z_{e - m}^i}& \cdots &{z_e^i} \end{array}} \right]$$ (20) 因此，基于
${\varGamma _i}$ 与${\varGamma _j}$ 轨迹之间的动态相似性，其相似概率${P_{ij}}$ 可定义为：$${P_{ij}}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} { - \infty }&{{\text{如果}}{\varGamma _i}\;{\text{和}}\;{\varGamma _j}{\text{冲突}}}\\ {\dfrac{{{\rm{rank}}\left( {{H_{{\varGamma _i}}}} \right) + {\rm{rank}}\left( {{H_{{\varGamma _j}}}} \right)}}{{{\rm{rank}}\left( {{H_{{\varGamma _{ij}}}}} \right)}} - 1}&{\text{其余情况}} \end{array}} \right.$$ (21) -
利用Hankel矩阵对轨迹之间的相似性进行判断可以识别出动态特性差别明显的轨迹，但对于动态特征本身就很接近的不同轨迹无法进行区分。因为Hausdorff距离可描述两组点集之间的相似程度，又因为同一飞行器上轨迹之间的几何形状具有相似性的特征，因此可以采用Hausdorff距离评价上述动态相似性判断后的所有轨迹。
对于轨迹
${\varGamma _i} = \left\{ {Z_i^1, \cdots ,Z_i^n} \right\}$ 与${\varGamma _j} = \left\{ {Z_j^1, \cdots ,Z_j^n} \right\}$ ，两者之间的Hausdorff距离可被表示为：$$H\left( {{\varGamma _i},{\varGamma _j}} \right) = \max \left( {h\left( {{\varGamma _i},{\varGamma _j}} \right),h\left( {{\varGamma _j},{\varGamma _i}} \right)} \right)$$ (22) 其中：
$$\begin{array}{l} h\left( {{\varGamma _i},{\varGamma _j}} \right) = \mathop {\max }\limits_{{Z_i} \in {\varGamma _i}} \mathop {\min }\limits_{{Z_j} \in {\varGamma _j}} \left\| {{Z_i} \cdot {Z_j}} \right\| \\ h\left( {{\varGamma _j},{\varGamma _i}} \right) = \mathop {\max }\limits_{{Z_j} \in {\varGamma _j}} \mathop {\min }\limits_{{Z_i} \in {\varGamma _i}} \left\| {{Z_j} \cdot {Z_i}} \right\| \\ \end{array} $$ (23) 式中：
$\left\| \cdot \right\|$ 表示求欧氏距离；$h\left( {{\varGamma _i},{\varGamma _j}} \right)$ 表示两轨迹之间的相似性度量。最后，根据运动平滑性，飞行器在相邻时刻的位姿参数应保持相对一致性。如果用四元数
$q$ 定义相邻帧之间的姿态，则应满足如下约束：$$\left\{ {\begin{array}{*{20}{c}} {\Delta q = \left\| {{q_{k - 1}} - {q_k}} \right\|} \\ {\Delta T = \left\| {{T_{k - 1}} - {T_k}} \right\|} \end{array}} \right.$$ (24) 若同时满足两个条件，则可以认为候选的四条轨迹属于同一飞行器。
因为飞行器初始位置一般都相隔较远，通过GNNSF数据关联算法结合贝叶斯滤波即可实现跟踪与初始轨迹的产生。
-
为了实际验证文中提出的多目标跟踪算法，文中采用参考文献[17]中实验所采集的数据集进行验证。具体的实验流程如图3所示，图4中，黑色曲线为参考文献[17]的跟踪结果，文中提出算法与参考文献[17]的比较结果如图5所示。
图 3 多目标三维轨迹跟踪算法可行性验证实验流程
Figure 3. Experimental process of feasibility verification of multi-target 3D trajectory tracking algorithm
图 4 多飞行器跟踪误差分布
Figure 4. Tracking error distribution of multi-vehicle
由实验结果可知：（1）与参考文献[17]的跟踪结果相比，文中提出的多目标跟踪算法实现了对多目标的跟踪；（2）但两者轨迹之间并不完全重合，这主要是文中采用的跟踪算法为扩展卡尔曼滤波算法与参考文献[17]中的粒子滤波算法在跟踪精度上有所差距；（3）跟踪精度相较于参考文献[17]在10 mm以内，这主要是由于目标高动态的飞行特性导致文中基于扩展卡尔曼滤波算法的跟踪精度误差较大。
-
为了验证轨迹识别算法的合理性，文中通过仿真实验将识别效果可视化。在实验中使用MATLAB2018b软件在CPU为i7，主频3.60 GHz，内存为8 GB的个人计算机进行仿真。合作靶标点的3D定位误差利用均值为0 mm，方差为2 mm的高斯白噪声进行模拟。首先在空间当中仿真生成三个飞行器，每一飞行器上有四个合作靶标点，在初始时刻假设每一飞行器之间的距离相对于每一飞行器上合作靶标之间的距离都较大，然后利用GNNSF算法进行合作靶标点的跟踪，得到12条待识别的3D轨迹。3D轨迹分布如图6所示。
图 6 轨迹识别示意图
Figure 6. Schematic diagram of trajectory recognition
首先根据模拟出来的每一条三维轨迹构造Hankel矩，并求解相应的矩阵的秩，其结果如表1所示。
表 1 多目标跟踪3D轨迹秩
Table 1. Multi-target tracking 3D trajectory rank
Cooperative target point label Drone 1# 2# 3# 4# Drone 1# 2 2 2 2 Drone 2# 2 2 2 2 Drone 3# 3 3 3 3 由图6和表1可知：（1）飞行器在空间中的分布相对同一飞行器上的合作靶标之间的距离较远；（2） 3#飞行器上合作靶标点的3D轨迹相对于其他飞行器具有更加复杂的运动，且由表中结果显示其Hankel矩阵的秩为3，大于其他两个飞行器上合作靶标的值，因此对于大数目的多目标跟踪，可以利用其排除一些识别轨迹，减小计算量；（3）表中结果显示1#飞行器与2#飞行器上合作靶标点的3D轨迹具有相同的Hankel矩阵秩，但图中显示其曲线复杂度明显不一样，这表明Hankel矩阵秩只能区别出运动复杂度较大的轨迹。
然后，根据轨迹之间的几何相似性，计算经过Hankel矩阵秩后剩余轨迹之间的Hausdorff距离，其结果如图7所示。
图 7 轨迹之间的Hausdorff距离
Figure 7. Hausdorff metric between trajectories
由图7可知：（1）所有待识别轨迹之间的Hausdorff距离分为两部分，阈值范围内的部分为满足识别条件的轨迹；（2）根据阈值范围内部分的轨迹编号可以直接求解交集即可实现多飞行器上合作靶标点的多轨迹的识别与注册。
-
为了验证算法精度，搭建了多目标跟踪实验环境。将三个同样构造的飞行器分别固定在位姿给定装置上，其中飞行器上合作靶标采用锂电池供电的高亮型发光二极管，分布在飞行器骨架的端点。位姿给定装置为旋转平台，通过控制位姿给定装置做单轴圆周旋转运动，同时利用摄像机采集主动发光式合作靶标的三维坐标，采用参考文献[18]的方法进行高精度的3D重建，并采用文中提出的多目标跟踪算法实现对测量视场内多目标的三维跟踪。其中飞行器的尺寸为400 mm，采用的摄像机为Flare 4M140，传感器尺寸为2048 pixel×2 048 pixel，像元大小为5.5 μm， 镜头为CHIOPT HC1605A，焦距为
$f = 12.5$ mm的定焦镜头。对于参考数据利用重建出来的三维数据采样人工观察的方式在全圆轨迹中均匀的挑选出10个代表点进行圆拟合作为误差计算的参考。其中三维跟踪算法精度的评估，如图8所示，采用测量点到其与圆弧中心之间连线与圆弧交点的最短距离的均方根作为评估指标：
图 8 圆形跟踪误差计算示意图
Figure 8. Circular tracking error calculation schematic
$${d_i} = \sqrt {{{\left( {x_c^i - x_m^i} \right)}^2} + {{\left( {y_c^i - y_m^i} \right)}^2} + {{\left( {z_c^i - z_m^i} \right)}^2}} $$ (25) 如图9所示，三个飞行器上合作靶标点在摄像机中的成像位置有相互交互等现象，这可模拟实际多飞行器运动室内定位中飞行器靠近、遮挡等相互作用。
图 9 实际实验中采集的靶标点图像
Figure 9. Target point images collected in actual experiments
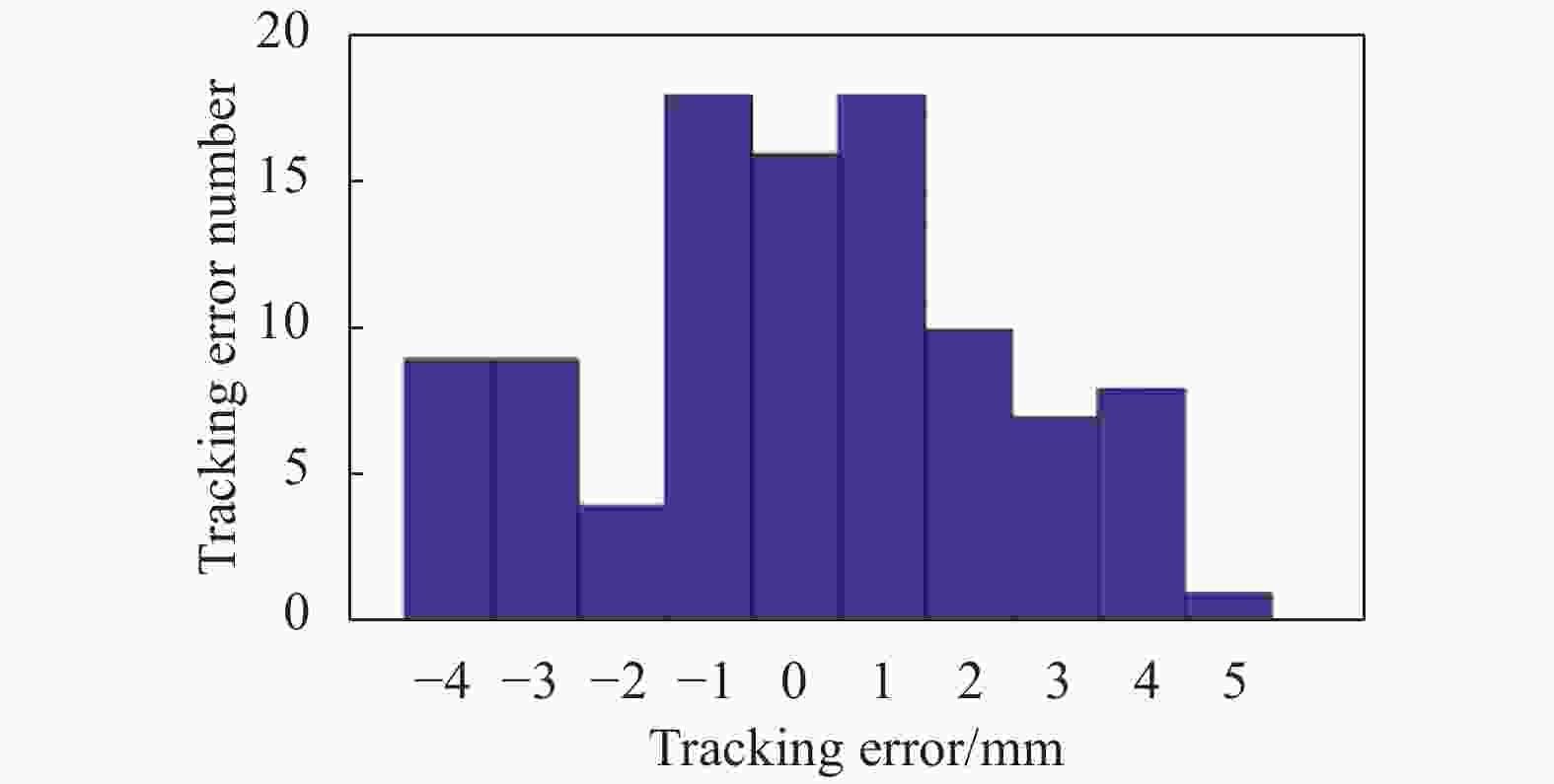
图10显示了文中跟踪算法对多飞行器上某一合作靶标点的跟踪精度，由图10可知，3D跟踪误差为4 mm（3σ），实现了对多飞行器上合作靶标点的跟踪要求。跟踪误差分布的不均衡是由于在选择参考轨迹拟合点时所引入了一定的偏差所导致。但整体跟踪精度可以满足需求，这也说明文中提出的算法对于运动轨迹相对平滑的目标跟踪具有较高的精度。
图 10 多飞行器跟踪误差分布
Figure 10. Tracking error distribution of multi-vehicle
-
为了解决多飞行器位姿估计中存在外观差异情况下、相互交叉频繁的多目标三维轨迹跟踪识别问题，文中从运动目标轨迹平滑性与同一飞行器上运动轨迹几何相似性两个假设出发，提出了一种基于时空一致性的多目标三维轨迹跟踪算法与一个基于Hankel轨迹矩阵秩和Hausdorff距离的运动轨迹粗细识别结合策略，有效地实现了对多飞行器合作靶标点的三维轨迹跟踪识别。
此外，考虑到文中所提出的三维轨迹跟踪算法采用的是基于贝叶斯滤波框架下的扩展卡尔曼滤波算法，因此对算法的跟踪精度与运动目标的动态特性有关。当跟踪目标具有较高的动态属性时，位移矢量变化很大，文中跟踪算法的精度会降低，位移矢量一致的约束也可能会失效。计划后续将引进基于粒子滤波等跟踪算法的多目标三维轨迹跟踪，提高跟踪精度，并考虑高阶的约束条件进行高动态的多飞行器运动参数测量。
Three-dimensional trajectory tracking recognition of multiple vehicles under displacement vector consistency
-
摘要: 合作靶标点三维轨迹的跟踪识别是实现室内环境中多飞行器位姿估计的关键，为此，提出了一种基于时空一致条件下的多目标三维轨迹跟踪识别算法。该方法包括运动轨迹跟踪与识别两部分，对于合作靶标点三维轨迹跟踪，提出了一种基于运动目标位移矢量一致的数据关联方法，该方法首先利用运动平滑性假设计算得到的数据关联概率值，结合匈牙利算法求解得到目标的数据关联关系，然后在贝叶斯滤波框架下实现合作靶标点的三维轨迹跟踪。对于合作靶标点的三维轨迹识别，又可以分为粗细两部分，利用运动轨迹Hankel矩阵的秩实现运动轨迹的粗识别，利用运动轨迹之间的Hausdorff距离实现运动轨迹的细识别，最终实现对每一个飞行器的轨迹识别与注册。实验结果表明，在三维测量手段为机器视觉，测量空间大小为2 m×2 m×2 m，提出的多目标跟踪算法的三维轨迹跟踪误差小于4 mm（3σ）时，轨迹识别正确率为100%。因此，所提出的算法可以有效地实现多飞行器上合作靶标点三维轨迹的跟踪识别。Abstract: The tracking and recognition of the three-dimensional trajectories of cooperative target points is the key to the estimation of the position and attitude of multi-aircraft in an indoor environment. Therefore, a multi-target three-dimensional trajectory tracking and recognition algorithm based on time and space consistent conditions was proposed. This method included two parts of motion trajectory tracking and recognition. For the three-dimensional trajectory tracking of cooperative target points, a data association method based on the consistency of the displacement vector of the moving target was proposed. This method first used the data association probability calculated by the motion smoothness assumption. Combined with the Hungarian algorithm to solve the target data association relationship, and then the three-dimensional trajectory tracking of cooperative target points under the Bayesian filter framework was realized. The three-dimensional trajectory recognition of cooperative target points was divided into two parts: the rank of the motion trajectory Hankel matrix to realize the coarse recognition of the motion trajectory, and the Hausdorff distance between the motion trajectories to realize the fine recognition of the motion trajectory. Eventually the trajectory recognition and registration of each aircraft was realized. Under the experimental conditions of computer vision measurement method and 2 m×2 m×2 m measurement space, the results show that the proposed multi-target tracking algorithm has a three-dimensional trajectory tracking error of less than 4 mm (3σ), and the trajectory recognition accuracy rate is 100%. Therefore, the proposed algorithm can effectively realize the tracking and recognition of the three-dimensional trajectory of cooperative target points on multi-aircraft.
-
Key words:
- multi-target tracking /
- trajectory recognition /
- data association /
- vector consistency
-
图 1 基于位移矢量一致的飞行器三维跟踪示意图
Figure 1. Schematic diagram of three-dimensional aircraft tracking based on consistent displacement vector
图 3 多目标三维轨迹跟踪算法可行性验证实验流程
Figure 3. Experimental process of feasibility verification of multi-target 3D trajectory tracking algorithm
表 1 多目标跟踪3D轨迹秩
Table 1. Multi-target tracking 3D trajectory rank
Cooperative target point label Drone 1# 2# 3# 4# Drone 1# 2 2 2 2 Drone 2# 2 2 2 2 Drone 3# 3 3 3 3 
下载: 导出CSV
-
[1] Wei Daozhi, Xiao Jun. Double satellite multi-target tracking algorithm based on BPGM-SME and improved UKF[J]. Infrared and Laser Engineering, 2017, 46 (S1): S113002. (in Chinese). [2] Doellinger J, Prabhakaran V S, Fu L, et al. Environment- aware multi-target tracking of pedestrians [J]. IEEE Robotics and Automation Letters, 2019, 4(2): 1831-1837. doi: 10.1109/LRA.2019.2898039 [3] Yoon K, Song Y, Jeon M. Multiple hypothesis tracking algorithm for multi-target multi-camera tracking with disjoint views [J]. IET Image Processing, 2018, 12(7): 1175-1184. doi: 10.1049/iet-ipr.2017.1244 [4] Song Ce, Zhang Bao, Song Yulong, et al. T-S tracking algorithm based on context auxiliary feature[J]. Opt Precision Eng, 2018, 26(8): 2122-2131 (in Chinese) [5] Emami P, Pardalos P M, Elefteriadou L, et al. Machine learning methods for solving assignment problems in multi-target tracking[J]. arXiv preprint arXiv, 2018: 1802.06897. [6] Zhang Guiyang, Huo Ju, Yang Ming, et al. Bidirectional closed cloud control for stereo vision measurement based on multi-source data[J]. Acta Optica Sinica, 2020, 40(19): 1915002. (in Chinese) [7] Li Yunhui, Huo Ju, Yang Ming. Research on posture estimation method of small-size vehicle in the ground test based on the graph optimal model[J]. Infrared and Laser Engineering, 2020, 49(4): 0413003. (in Chinese) [8] Hamid Rezatofighi S, Milan A, Zhang Z, et al. Joint probabilistic data association revisited[C]//Proceedings of the IEEE International Conference on Computer Vision, 2015: 3047-3055. [9] Kim C, Li F, Ciptadi A, et al. Multiple hypothesis tracking revisited[C]// Proceedings of the IEEE International Conference on Computer Vision, 2015: 4696-4704. [10] Oh S, Russell S, Sastry S. Markov chain Monte Carlo data association for multi-target tracking [J]. IEEE Transactions on Automatic Control, 2009, 54(3): 481-497. doi: 10.1109/TAC.2009.2012975 [11] Keuper M, Tang S, Andres B, et al. Motion segmentation & multiple object tracking by correlation co-clustering [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 42(1): 140-153. [12] Gong Junliang, He Xin, Wei Zhonghui, et al. Multiple infrared target tracking using improved auxiliary particle filter[J]. Opt Precision Eng, 2012, 20(2): 413-421. (in Chinese) [13] Fu Ying, Tang Ziyue, Sun Yongjian. Methodology for tracking multi-target hidden in Doppler blind zone based on airborne and ground-based early warning radar cooperation[J]. Infrared and Laser Engineering, 2014, 43(7): 2379-2386. (in Chinese) [14] Betke M, Wu Z. Data association for multi-object visual tracking [J]. Synthesis Lectures on Computer Vision, 2016, 6(2): 1-120. doi: 10.2200/S00726ED1V01Y201608COV009 [15] Rasmussen C, Hager G D. Probabilistic data association methods for tracking complex visual objects [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2001, 23(6): 560-576. [16] Breiman L. Hinging hyperplanes for regression, classification, and function approximation [J]. IEEE Transactions on Information Theory, 1993, 39(3): 999-1013. doi: 10.1109/18.256506 [17] Cheng X E, Qian Z M, Wang S H, et al. A novel method for tracking individuals of fruit fly swarms flying in a laboratory flight arena [J]. PloS one, 2015, 10(6): e0129657. [18] Li Yunhui, Huo Ju, Liu Jia, et al. Calibration of quad-camera measurement systems using a one-dimensional calibration object for three-dimensional point reconstruction [J]. Optical Engineering, 2019, 58(6): 1. -
点击查看大图
图(10) / 表(1)
计量
- 文章访问数: 247
- HTML全文浏览量: 44
- PDF下载量: 27
- 被引次数: 0
